
【题目】在△ABC中,D、E分别是边AB、BC上的点,AE和CD交于点F,且∠CFE=∠B。
(1)如图1,求证:∠AEC=∠CDB;

(2)如图2,过点C作CG⊥AC,交AB于点G,CD⊥CB,∠ACD =∠CAB-∠B,求证:AC=GC;

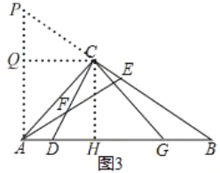
(3)如图3,在(2)的条件下,CE+CD=AE,CG=![]() ,求线段BC的长。
,求线段BC的长。

【答案】(1)见解析(2)见解析(3)2.
【解析】
(1)在△CEF中,∠ECF+∠CFE+∠CEF=180°,进而得到∠ECF+∠B+∠CEF=180°,在△BCD中,∠BCD+∠B+∠CDB=180°,即可得到结论;
(2)先判断出∠ACD=∠BCG,再根据∠AGC=∠B+∠BCG,即可得到结论;
(3)先判断出四边形AHCQ是正方形,得到CH=CQ,再判断出△CQP≌△CHD,得到∠CPQ=∠CDH,CP=CD,进而得到PE=AE,即∠P=∠PAE,根据(1)的结论,∠AEC=∠CDB得到∠AEC=∠P=∠PAE,即∠P=60°,再求出∠B=90°-∠P=30°,根据含30°的直角三角形的性质即可求解.
(1)在△CEF中,∠ECF+∠CFE+∠CEF=180°,
∵∠CFE=∠B
∴∠ECF+∠B+∠CEF=180°,
在△BCD中,∠BCD+∠B+∠CDB=180°,
∴∠AEC=∠CDB;
(2)∵CG⊥AC,BC⊥CD,
∴∠ACG=∠BCD=90°,
∴∠ACD=∠BCG,
∵∠ACD+∠B=∠CAB,
∴∠BCG +∠B=∠CAB
∴∠AGC=∠B+∠BCG,
∴∠CAB=∠AGC
∴AC=AG;
(3)如图3,过点C作CH⊥AB于H,过点A作AP⊥AB与BC的延长线交于点P,过点C作CQ⊥AP于Q,
∴四边形AHCQ是矩形,
∴∠HCQ=90°,
由(2)知,AC=CG,∠ACG=90°,
∴CH=AH,
∴矩形AHCQ是正方形,
∴CH=CQ,
∵∠HCQ=90°,
∴∠PCQ+∠BCH=90°,
∵∠BCD=90°,
∴∠DCH+∠BCH=90°
∴∠PCQ=∠DCH
∵∠CQP=∠CHD=90°,
∴△CQP≌△CHD(ASA),
∴∠CPQ=∠CDH,CP=CD,
∵CD+CE=AE,
∴CP+CE=AE,
∴PE=AE,
∴∠P=∠PAE,
根据(1)可知∠AEC=∠CDB
∵∠CPQ=∠CDH,
∴∠AEC=∠P=∠PAE,
∴∠P=60°,
∴∠B=90°-∠P=30°,
在Rt△CHG中,CH=![]() =1,
=1,
在Rt△CHB中,BC=2CH=2.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:初中数学 来源: 题型:
【题目】如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60,请你探究OE,EF之间有什么数量关系?并证明你的结论。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平面直角坐标系中,抛物线y=ax2+bx+3与x轴的两个交点分别为A(﹣3,0),B(1,0),与y轴的交点为D,对称轴与抛物线交于点C,与x轴负半轴交于点H.

(1)求抛物线的表达式;
(2)点E,F分别是抛物线对称轴CH上的两个动点(点E在点F上方),且EF=1,求使四边形BDEF的周长最小时的点E,F坐标及最小值;
(3)如图2,点P为对称轴左侧,x轴上方的抛物线上的点,PQ⊥AC于点Q,是否存在这样的点P使△PCQ与△ACH相似?若存在请求出点P的坐标,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠ACB =90°,∠A=30°,点D在直线AC上,CD=CB,点E在线段AC上,AE=2EC,连接EB、BD,则∠EBD=____________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D、E在△ABC的BC边上,BD=CE,AD=AE。

(1)如图1,求证:∠BAD=∠CAE;
(2)如图2,若点E在AC的垂直平分线上,∠C=36°,直接写出图中所有的等腰三角形。
查看答案和解析>>
科目:初中数学 来源: 题型:
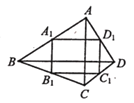
【题目】如图,四边形ABCD的两条对角线AC、BD互相垂直, A1B1C1D1, 是四边形ABCD的中点四边形,如果AC=8, BD=10,那么四边形A1B1C1D1,的面积为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地开往B地,全程800km;所行的路程与时间的函数图像如图所示,下列问题:①乙车比甲车早出发2h;②甲车追上乙车时行驶了300km;③乙车的速度小于甲车速度;④甲车跑完全程比乙车跑完全程少用3h;以上正确的序号是_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
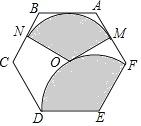
【题目】如图,点O为正六边形ABCDEF的中心,点M为AF中点,以点O为圆心,以OM的长为半径画弧得到扇形MON,点N在BC上;以点E为圆心,以DE的长为半径画弧得到扇形DEF,把扇形MON的两条半径OM,ON重合,围成圆锥,将此圆锥的底面半径记为r1;将扇形DEF以同样方法围成的圆锥的底面半径记为r2,则r1:r2=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费,分两档收费:第一档是当月用电量不超过240度时实行“基础电价”;第二档是当用电量超过240度时,其中的240度仍按照“基础电价”计费,超过的部分按照“提高电价”收费.设每个家庭月用电量为x 度时,应交电费为y 元.具体收费情况如折线图所示,请根据图象回答下列问题:
(1)“基础电价”是____________元 ![]() 度;
度;
(2)求出当x>240 时,y与x的函数表达式;
(3)若紫豪家六月份缴纳电费132元,求紫豪家这个月用电量为多少度?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com