
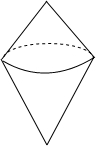
 如图所示的几何体左视图是( )
如图所示的几何体左视图是( )| A. | 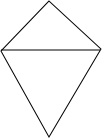 | B. | 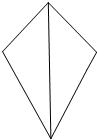 | C. | 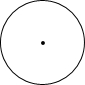 | D. |  |
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
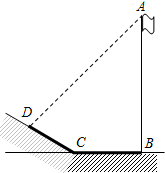 为了测量操场边上旗杆的高度,学习小组在一个阳光明媚的时候带着测量工具来到旗杆下,此时发现旗杆顶端A的影子落在旗杆附近一段坡角为30°的斜坡上的点D处,并测得太阳光线与斜坡的夹角∠ADC=75°,旗杆影子落在操场上的长BC=5米,落在斜坡上的长CD=6米.
为了测量操场边上旗杆的高度,学习小组在一个阳光明媚的时候带着测量工具来到旗杆下,此时发现旗杆顶端A的影子落在旗杆附近一段坡角为30°的斜坡上的点D处,并测得太阳光线与斜坡的夹角∠ADC=75°,旗杆影子落在操场上的长BC=5米,落在斜坡上的长CD=6米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
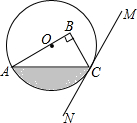 如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,OA为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A.
如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,OA为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
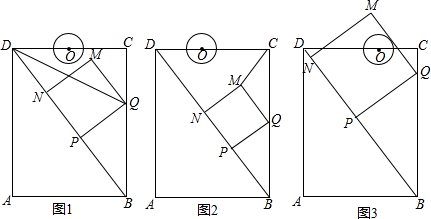
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | x | C. | $\frac{1}{x}$ | D. | $\frac{x+2}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -4 | B. | $\frac{1}{4}$ | C. | -$\frac{1}{4}$ | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com