
【题目】如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,在AD上截取AE=AB,连接BE,EO,并求∠BEO的角度(要求:尺规作图,保留痕迹,不写作法)

 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
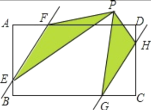
【题目】如图,在矩形ABCD中,AD=6,AB=5,点E、F、G、H分别在AD、AB、BC、CD上,且AF=CG=1,BE=DH=2,点P是直线EF、GH之间任意一点,连接PE、PF、PG、PH,则△PEF和△PGH的面积和等于______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,设甲、乙、丙、丁分别表示△ABC,△ACD,△EFG,△EGH.已知∠ACB=∠CAD=∠EFG=∠EGH=70°,∠BAC=∠ACD=∠EGF=∠EHG=50°,则叙述正确的是( )
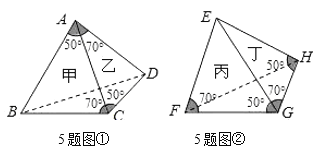
A.甲、乙全等,丙、丁全等B.甲、乙全等,丙、丁不全等
C.甲、乙不全等,丙、丁全等D.甲、乙不全等,丙、丁不全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】丹尼斯超市举行有奖促销活动:顾客凡一次性购买满![]() 元者即可获得一次摇奖机会.摇奖机是一个圆形转盘,被等分成
元者即可获得一次摇奖机会.摇奖机是一个圆形转盘,被等分成![]() 个扇形,如果转盘停止后,指针正好对准红黄或蓝色区域,顾客就可以分别获得一、二、三等奖奖金依次为
个扇形,如果转盘停止后,指针正好对准红黄或蓝色区域,顾客就可以分别获得一、二、三等奖奖金依次为![]() 元、
元、![]() 元、
元、![]() 元一次性购物满
元一次性购物满![]() 元者,如果不摇奖可返还奖金
元者,如果不摇奖可返还奖金![]() 元.
元.

(1)摇奖一次,获一等奖、二等奖、三等奖的概率分别是多少?
(2)小李一次性购物满![]() 元他是参与摇奖划算,还是领
元他是参与摇奖划算,还是领![]() 元现金划算?请你帮他算算
元现金划算?请你帮他算算
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m).
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完全平方公式:(a±b)2=a2±2ab+b2适当的变形,可以解决很多的数学问题.
例如:若a+b=3,ab=1,求a2+b2的值.
解:因为a+b=3,ab=1
所以(a+b)2=9,2ab=2
所以a2+b2+2ab=9,2ab=2
得a2+b2=7
根据上面的解题思路与方法,解决下列问题:
(1)若(7﹣x)(x﹣4)=1,求(7﹣x)2+(x﹣4)2的值;
(2)如图,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设AB=5,两正方形的面积和S1+S2=17,求图中阴影部分面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
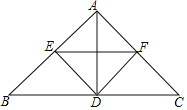
【题目】如图,在△ABC中,AB=AC,D是边BC上的一点,DE⊥AB,DF⊥AC,垂足分别是E、F,EF∥BC.
(1)求证:△BDE≌△CDF;
(2)若BC=2AD,求证:四边形AEDF是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+b与坐标轴交于C,D两点,直线AB与坐标轴交于A,B两点,线段OA,OC的长是方程x2﹣3x+2=0的两个根(OA>OC).
(1)求点A,C的坐标;
(2)直线AB与直线CD交于点E,若点E是线段AB的中点,反比例函数y=![]() (k≠0)的图象的一个分支经过点E,求k的值;
(k≠0)的图象的一个分支经过点E,求k的值;
(3)在(2)的条件下,点M在直线CD上,坐标平面内是否存在点N,使以点B,E,M,N为顶点的四边形是菱形?若存在,请直接写出满足条件的点N的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com