练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

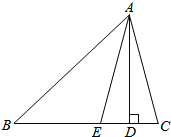
    【题目】如图，AD是△ABC的BC边上的高，AE平分∠BAC，若∠B＝42°，∠C＝70°，求∠AEC和∠DAE的度数．

    【答案】∠DAE＝14°，∠AEC＝76°.

    【解析】

    由三角形内角和定理可求得∠BAC的度数，在Rt△ADC中，可求得∠DAC的度数，AE是角平分线，有∠EAC＝∠BAC，故∠EAD＝∠EAC﹣∠DAC，∠AEC＝90°﹣∠EAD．

    解：∵∠B＝42°，∠C＝70°，

    ∴∠BAC＝180°﹣∠B﹣∠C＝68°，

    ∵AE是角平分线，

    ∴∠EAC＝∠BAC＝34°．

    ∵AD是高，∠C＝70°，

    ∴∠DAC＝90°﹣∠C＝20°，

    ∴∠EAD＝∠EAC﹣∠DAC＝34°﹣20°＝14°，∠AEC＝90°﹣14°＝76°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，点A、点B是双曲线图象上的两点（A在B的右侧）.延长AB交y轴正半轴于C，OC的中点为D.连结AO，BO，交点为E.若△BEO的面积为4，四边形AEDC的面积等于△BEO的面积，则k的值为_______.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图：矩形ABCD中，AB=2，BC=5，E、P分别在AD、BC上，且DE=BP=1．

    （1）判断△BEC的形状，并说明理由？

    （2）判断四边形EFPH是什么特殊四边形？并证明你的判断；

    （3）求四边形EFPH的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，D是等边三角形ABC内一点，将线段AD绕点A顺时针旋转60°，得到线段AE，连接CD，BE．

    （1）求证：∠AEB=∠ADC；

    （2）连接DE，若∠ADC=105°，求∠BED的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

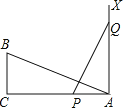
    【题目】如图，在Rt△ABC中，∠C＝90°，AC＝12cm，BC＝6cm，一条线段PQ＝AB，P，Q两点分别在线段AC和AC的垂线AX上移动，若以A、B、C为顶点的三角形与以A、P、Q为顶点的三角形全等，则AP的值为（　　）

    A.6cmB.12cm

    C.12cm或6cmD.以上答案都不对

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，点A、D在y轴正半轴上，点B、C分别在x轴上，CD平分∠ACB与y轴交于D点，∠CAO＝90°﹣∠BDO．

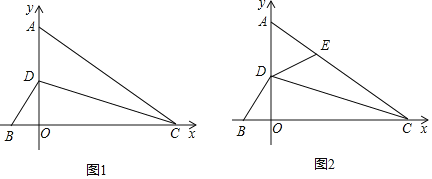
    （1）求证：AC＝BC；

    （2）如图2，点C的坐标为（4，0），点E为AC上一点，且∠DEA＝∠DBO，求BC+EC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD，点E，F分别在AD，CD上，BG⊥EF，点G为垂足，AB=5a，AE=a，CF=2a，则BG长是（ ）

    A. a B. a C. a D. a

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，平面直角坐标的原点是等边三角形的中心，A（0，1），把△ABC绕点O顺时针旋转，每秒旋转60°，则第2017秒时，点A的坐标为（　　）

    A. （0，1） B. （﹣，﹣） C. （，） D. （，﹣）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读下面的文字后回答问题：

    我们知道无理数是无限不循环小数，例如＝1.414…，的小数部分我们无法全部出来，但可以用﹣1来表示．

    请解答下列问题：

    （1）的整数部分是　 　，小数部分是　 　．

    （2）若的小数部分是a，的整数部分是b，求a（b+）的值．

    （3）9﹣的小数部分是a，4+的整数部分是b，求a（b+）的立方根．

    查看答案和解析>>

    同步练习册答案