练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．求代数式|x+5|+|2x-4|的最小值．

    分析 要化简已知的代数式中的绝对值，考虑x+5与2x-4的正负，分三种情况考虑：①x＜-5；②-5≤x≤2；③x＞2，利用绝对值的代数意义化简，即可得到代数式的最小值．

    解答 解：：①x＜-5，
    |x+5|+|2x-4|
    =-x-5-2x+4
    =-3x-1＜14；
    ②-5≤x≤2，
    |x+5|+|2x-4|
    =x+5-2x+4
    =-x+9≤7；
    ③x＞2，
    |x+5|+|2x-4|
    =x+5+2x-4
    =3x+1＞7．
    综上可知，代数式|x+5|+|2x-4|的最小值是7．

    点评 此题考查了绝对值的代数意义，即正数的绝对值等于它本身；负数的绝对值等于它的相反数；0的相反数还是0，分类讨论绝对值里式子的正负是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    13．观察等式5-1=4，6-2=4，7-3=4，8-4=4…，这些等式反映某些数之间的某种规律，设n表示自然数，试用含n的等式表示这个规律为（n+4）-n=4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．已知$\frac{a}{3}$=$\frac{b}{4}$=$\frac{c}{5}$≠0，求代数式$\frac{2a+b+c}{2b-a}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．计算：$\frac{1}{2}$$+\frac{1}{4}$$+\frac{1}{8}$$+…+\frac{1}{1024}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．进价为每件40元的某商品，当售价为每件50元时，每星期可以卖出500件．市场调查反映：如果每件商品每降价1元，每星期可多卖出10件；如果每件商品每涨价1元，则每星期少卖出5件，公司规定：每件商品的售价不能低于每件42元，且每星期至少要销售该商品400件，设每件售价x元（x为正整数），每星期销售量为y件．
    （1）求y与x的函数关系及自变量x的取值范围．
    （2）设商场每星期销售该商品的利润为w，请求出w与x的函数关系式．
    （3）当该商品的售价定为多少元时，才能使每星期利润最大？并求这个最大利润．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．观察日历可以发现横排相邻的两个日期数大小相差1，上、下相邻的两个日期数相差7；若横排相邻的两个日期数之和为15，设较小的一个日期数为x，则可列方程x+x+1=15．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

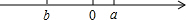    15．已知数a，b在数轴上对应点的位置如图所示，则下列结论正确的是②③④⑤⑥（填序号）．
    ①a+b＞0；②|a|＜|b|；③ab＜0；
    ④$\frac{b}{a}$＜0；⑤a-b＞0；⑥b-a＜0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．下列说法错误的是（　　）
    A．由一个平面图形得到它的轴对称图形叫作轴对称变换
    B．将一个图形沿一条直线折叠叫作轴对称变换
    C．对称轴方向和位置发生变化时，得到的图形方向和位置也发生变化
    D．成轴对称的两个图形中的任何一个可以看作由另一个图形经过轴对称变换后得到

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．已知任意四边形ABCD，边AD、BC的中点分别为E、F，求证：$\overrightarrow{EF}$=$\frac{1}{2}$（$\overrightarrow{AB}$$+\overrightarrow{DC}$）．

    查看答案和解析>>

    同步练习册答案