
分析 (1)设购进甲商品x件,乙商品y件,根据进价36000元及利润6000元即可得出关于x、y的二元一次方程组,解之即可得出结论;
(2)根据总利润=甲种商品利润+乙种商品利润即可得出y关于x的一次函数关系式,根据一次函数的性质即可得出结论.
解答 解:(1)设购进甲商品x件,乙商品y件,
依题意得:$\left\{\begin{array}{l}{120x+100y=36000}\\{(130-120)x+(150-100)y=6000}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=240}\\{y=72}\end{array}\right.$.
答:该商场购进甲商品240件,乙商品72件.
(2)依题意得:y=(130-120)x+(150-100)(100-x)=-40x+5000.
∵-40<0,
∴购进甲种商品件数x逐渐增加时,利润y逐渐减少.
点评 本题考查了一次函数的应用、解二元一次方程组以及一次函数的性质,根据数量关系列出二元一次方程组(或一次函数关系式)是解题的关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
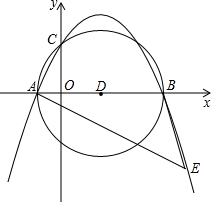 如图,在平面直角坐标系内,点O为坐标原点,抛物线y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4交x轴负半轴于点A,交x轴正半轴于点B,交y轴于点C.
如图,在平面直角坐标系内,点O为坐标原点,抛物线y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4交x轴负半轴于点A,交x轴正半轴于点B,交y轴于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
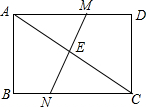 如图,在矩形ABCD中,AC是对角线,E是AC的中点,过E作MN交AD于M,交BC于N.
如图,在矩形ABCD中,AC是对角线,E是AC的中点,过E作MN交AD于M,交BC于N.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
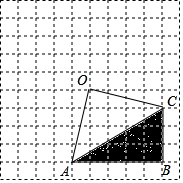 如图,在网格中有一个四边形图案.
如图,在网格中有一个四边形图案.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
| 甲班 | 100 | 98 | 102 | 97 | 103 | 500 |
| 乙班 | 99 | 100 | 95 | 109 | 97 | 500 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
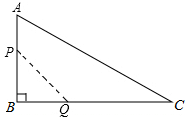 如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向点B以2mm/s的速度移动,动点Q从B点开始沿边BC向点C以4mm/s的速度移动.如果P、Q两点同时出发,那么△PBQ的面积S随时间t的函数关系式是S=24t-4t2(0≤t≤6)(写出t的取值范围)
如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB向点B以2mm/s的速度移动,动点Q从B点开始沿边BC向点C以4mm/s的速度移动.如果P、Q两点同时出发,那么△PBQ的面积S随时间t的函数关系式是S=24t-4t2(0≤t≤6)(写出t的取值范围)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com