
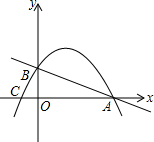
 如图,已知直线y=-$\frac{1}{2}$x+2与x轴、y轴分别相交于A、B两点,过A、B两点的抛物线y=ax2+bx+c交x轴于点C(-1,0).
如图,已知直线y=-$\frac{1}{2}$x+2与x轴、y轴分别相交于A、B两点,过A、B两点的抛物线y=ax2+bx+c交x轴于点C(-1,0).分析 (1)利用一次函数图象上点的坐标特征确定A点和B点坐标;
(2)设交点式y=a(x+1)(x-4),然后把B点坐标代入求出a即可得到所以抛物线解析式;
(3)设P(t,-$\frac{1}{2}$t2+$\frac{3}{2}$t+2)(-1<t<4),根据三角形面积公式得到$\frac{1}{2}$•(4+1)•(-$\frac{1}{2}$t2+$\frac{3}{2}$t+2)=2•$\frac{1}{2}$•2•4,由于此方程没有实数解,于是可判断抛物线在x轴上方部分不存在一点P,使得△ACP的面积是△ABO的2倍,然后把抛物线解析式配成顶点式即可得到使△ACP的面积最大的P点坐标.
解答 解:(1)当x=0时,y=-$\frac{1}{2}$x+2=2,则B(0,2),
当y=0时,-$\frac{1}{2}$x+2=0,解得x=4,则A(4,0),
(2)设抛物线解析式为y=a(x+1)(x-4),
把B(0,2)代入得a•1•(-4)=2,解得a=-$\frac{1}{2}$,
所以抛物线解析式为y=-$\frac{1}{2}$(x+1)(x-4),即y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2;
(3)不存在.
设P(t,-$\frac{1}{2}$t2+$\frac{3}{2}$t+2)(-1<t<4),
因为△ACP的面积是△ABO的2倍,
所以$\frac{1}{2}$•(4+1)•(-$\frac{1}{2}$t2+$\frac{3}{2}$t+2)=2•$\frac{1}{2}$•2•4,
整理得5t2-15t+12=0,△=152-4×5×12<0,方程没有实数解,
所以抛物线在x轴上方部分不存在一点P,使得△ACP的面积是△ABO的2倍,
当P点为抛物线的顶点时,△ACP的面积最大,
因为y=-$\frac{1}{2}$(x-$\frac{3}{2}$)2+$\frac{25}{8}$,
此时P点坐标为($\frac{3}{2}$,$\frac{25}{8}$).
点评 本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:解答题
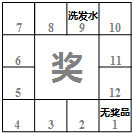 大商超市为了吸引顾客,设立了一个抽奖活动.如图,活动规则:顾客单票(每次)购物满100元,就能获得一次抽奖机会,且百分之百中奖.顾客同时掷两个骰子,数字朝上的点数之和是几,就能获得相应数字格子中的物品.
大商超市为了吸引顾客,设立了一个抽奖活动.如图,活动规则:顾客单票(每次)购物满100元,就能获得一次抽奖机会,且百分之百中奖.顾客同时掷两个骰子,数字朝上的点数之和是几,就能获得相应数字格子中的物品.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
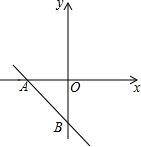 如图,在平面直角坐标系中,一次函数y=-x-3分别与x轴、y轴相交于A、B两点,二次函数y=x2+mx+n(m≠6)的图象经过点A.
如图,在平面直角坐标系中,一次函数y=-x-3分别与x轴、y轴相交于A、B两点,二次函数y=x2+mx+n(m≠6)的图象经过点A.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>1 | B. | x<$\frac{1}{4}$ | C. | $\frac{1}{4}$<x<1 | D. | 无解 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
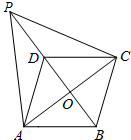 如图,在菱形ABCD中,对角线AC和BD相交于点O,点P是BD延长线上的一点.
如图,在菱形ABCD中,对角线AC和BD相交于点O,点P是BD延长线上的一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com