
 的两根.
的两根.
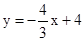 ;(2)(3,5)或(3,
;(2)(3,5)或(3,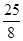 ).
). 得x1=3,x2=4.
得x1=3,x2=4.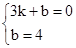 ,解得
,解得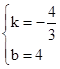 .
.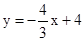 .
.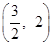 ,
,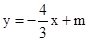 ,则
,则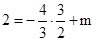 ,解得:
,解得: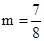 .
.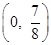 .
.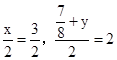 ,解得:x=3,y=
,解得:x=3,y=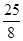 .
.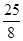 ).
).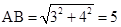 ,
,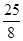 ).
).

科目:初中数学 来源:不详 题型:解答题
 在第一象限内的图象交于点B(m,n),连结OB.若S△AOB=6,S△BOC=2.
在第一象限内的图象交于点B(m,n),连结OB.若S△AOB=6,S△BOC=2.
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
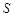 (单位:平方米)与工作时间
(单位:平方米)与工作时间 (单位:小时)的函数关系的图象如图所示,则休息后园林队每小时绿化面积为
(单位:小时)的函数关系的图象如图所示,则休息后园林队每小时绿化面积为
| A.40平方米 | B.50平方米 | C.80平方米 | D.100平方米 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.y=-0.5x+20 ( 0<x<20) | B.y=-0.5x+20 (10<x<20) |
| C.y=-2x+40 (10<x<20) | D.y=-2x+40 (0<x<20) |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 两地同时出发相向而行,其中甲到
两地同时出发相向而行,其中甲到 地后立即返回,下图是它们离各自出发地的距离
地后立即返回,下图是它们离各自出发地的距离 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数图象.
(小时)之间的函数图象. (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数关系式,并写出自变量的取值范围;
(小时)之间的函数关系式,并写出自变量的取值范围; 小时,求乙车离出发地的距离
小时,求乙车离出发地的距离 (千米)与行驶时间
(千米)与行驶时间 (小时)之间的函数关系式;
(小时)之间的函数关系式;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com