
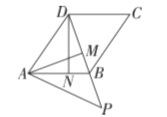
【题目】如图,在平行四边形![]() 中,连接
中,连接![]() ,且
,且![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,在
,在![]() 的延长线上取一点
的延长线上取一点![]() ,
,![]() ,若
,若![]() ,则
,则![]() 的度数为____________
的度数为____________![]() .
.
科目:初中数学 来源: 题型:
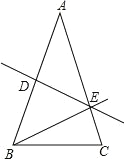
【题目】在△ABC 中,AB>BC,AB=AC,DE 是 AB 的垂直平分线,垂足为 D,交 AC 于 E.
(1)若∠ABE=40°,求∠EBC 的度数;
(2)若△ABC 的周长为 41cm,一边长为 15cm,求△BCE 的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
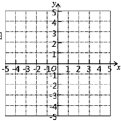
【题目】已知三角形![]() 的三个顶点坐标分别为
的三个顶点坐标分别为![]()
(1)在所给的平面直角坐标系中画出三角形![]()
(2)直接写出点A关于![]() 轴,
轴,![]() 轴的对称点坐标
轴的对称点坐标
(3)若在![]() 轴上找一点P,使得
轴上找一点P,使得![]() ,请在图中作出点P(尺规作图,不写作法,保留作图痕迹)
,请在图中作出点P(尺规作图,不写作法,保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】亮亮和颖颖住在同一幢住宅楼,两人准备用测量影子的方法测算其楼高,但恰逢阴天,于是两人商定改用下面方法:如图,亮亮蹲在地上,颖颖站在亮亮和楼之间,两人适当调整自己的位置,当楼的顶部![]() , 颖颖的头顶
, 颖颖的头顶![]() 及亮亮的眼睛
及亮亮的眼睛![]() 恰在一条直线上时,两人分别标定自己的位置
恰在一条直线上时,两人分别标定自己的位置![]() ,
, ![]() . 然后测出两人之间的距离
. 然后测出两人之间的距离![]() , 颖颖与楼之间的距离
, 颖颖与楼之间的距离![]() (
(![]() ,
, ![]() ,
, ![]() 在一条直线上),颖颖的身高
在一条直线上),颖颖的身高![]() , 亮亮蹲地观测时眼睛到地面的距离
, 亮亮蹲地观测时眼睛到地面的距离![]() . 你能根据以上测量数据帮助他们求出住宅楼的高度吗?
. 你能根据以上测量数据帮助他们求出住宅楼的高度吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过A(-3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.
经过A(-3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.
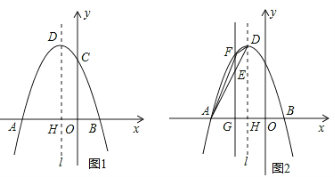
(1)求该抛物线的解析式;
(2)若点P是该抛物线对称轴l上的一个动点,求△PBC周长的最小值;
(3)如图(2),若E是线段AD上的一个动点( E与A、D不重合),过E点作平行于y轴的直线交抛物线于点F,交x轴于点G,设点E的横坐标为m,△ADF的面积为S.
①求S与m的函数关系式;
②S是否存在最大值?若存在,求出最大值及此时点E的坐标; 若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,![]() ,
,![]() 的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,
的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,![]() ,垂足为G,若
,垂足为G,若![]() ,则AE的边长为
,则AE的边长为![]()
![]()

A. ![]() B.
B. ![]() C. 4 D. 8
C. 4 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市防汛办为解决台风季排涝问题,准备在一定时间内铺设一条长4000米的排水管道,实际施工时,![]() .求原计划每天铺设管道多少米?题目中部分条件被墨汁污染,小明查看了参考答案为:“设原计划每天铺设管道x米,则可得方程
.求原计划每天铺设管道多少米?题目中部分条件被墨汁污染,小明查看了参考答案为:“设原计划每天铺设管道x米,则可得方程![]() =20,…”根据答案,题中被墨汁污染条件应补为( )
=20,…”根据答案,题中被墨汁污染条件应补为( )
A.每天比原计划多铺设10米,结果延期20天完成
B.每天比原计划少铺设10米,结果延期20天完成
C.每天比原计划多铺设10米,结果提前20天完成
D.每天比原计划少铺设10米,结果提前20天完成
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 为
为![]() 上的两个定点,
上的两个定点,![]() 是
是![]() 上的动点(
上的动点(![]() 不与
不与![]() 、
、![]() 重合),我们称
重合),我们称![]() 为
为![]() 上关于点
上关于点![]() 、
、![]() 的滑动角.已知
的滑动角.已知![]() 是
是![]() 上关于点
上关于点![]() 、
、![]() 的滑动角,
的滑动角,
(1)若![]() 为
为![]() 的直径,则
的直径,则![]() ________;
________;
(2)若![]() 半径为
半径为![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(3)若![]() 半径为
半径为![]() ,
,![]() ,
,![]() ,求
,求
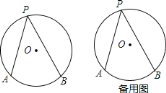
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com