
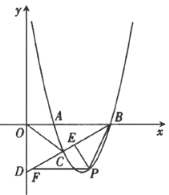
【题目】如图,抛物线![]() 与x轴交于A,B两点,抛物线上另有一点 C在x轴下方,且使ΔOCA∽ΔOBC.
与x轴交于A,B两点,抛物线上另有一点 C在x轴下方,且使ΔOCA∽ΔOBC.
(1)求线段OC的长度;
(2)设直线BC与y轴交于点D,点C是BD的中点时,求直线BD和抛物线的解析式,
(3)在(2)的条件下,点P是直线BC下方抛物线上的一点,过P作![]() 于点E,作PF//AB交BD于点F,是否存在一点P,使得
于点E,作PF//AB交BD于点F,是否存在一点P,使得![]() 最大,若存在,请求出该最大值;若不存在,请说明理由.
最大,若存在,请求出该最大值;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ,
,![]() ;(3)存在,
;(3)存在,![]() .
.
【解析】
(1)由抛物线![]() 与x轴交于A,B两点,得OA=1,OB=3,由ΔOCA∽ΔOBC.,得
与x轴交于A,B两点,得OA=1,OB=3,由ΔOCA∽ΔOBC.,得![]() ,进而得到答案;
,进而得到答案;
(2)由点C是BD的中点,OC=![]() ,得:a=
,得:a=![]() ,点C的坐标是:(
,点C的坐标是:(![]() ,
,![]() ),再根据待定系数法,求出直线BD和抛物线的的解析式;
),再根据待定系数法,求出直线BD和抛物线的的解析式;
(3)由直线BD的解析式为:![]() ,得:∠OBD=30°,由
,得:∠OBD=30°,由![]() ,PF//AB,得PE=
,PF//AB,得PE=![]() PF,
PF,![]() ,设P坐标为(m,
,设P坐标为(m,![]() ),(
),(![]() ),
),
点F的坐标为(![]() ,
,![]() ),求出PF关于m的函数解析式,即可求出
),求出PF关于m的函数解析式,即可求出![]() 的最大值.
的最大值.
(1)∵抛物线![]() 与x轴交于A,B两点,
与x轴交于A,B两点,
∴A(1,0),B(3,0),即:OA=1,OB=3,
∵ΔOCA∽ΔOBC.,
∴![]() ,即:
,即:![]() ,
,
∴OC=![]() ;
;
(2)∵点C是BD的中点,
∴点C的坐标(![]() ,
,![]() ),
),
∵OC=![]() ,
,
∴![]() ,解得:a=
,解得:a=![]() 或a=-
或a=-![]() (舍去)
(舍去)
∴抛物线的解析式为:![]() ,
,
即:![]()
∴点C的坐标是:(![]() ,
,![]() ),
),
设直线BD的解析式为:y=kx+b,
把(![]() ,
,![]() ),(3,0)代入y=kx+b,
),(3,0)代入y=kx+b,
得: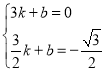 ,解得:
,解得: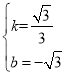 ,
,
∴直线BD的解析式为:![]() ;
;
(3)存在,理由如下:
∵直线BD的解析式为:![]() ,
,
∴点D坐标为(0,![]() ),即:OD=
),即:OD=![]() ,
,
∴tan∠OBD=![]() ,
,
∴∠OBD=30°,
∵![]() ,PF//AB,
,PF//AB,
∴∠PFE=∠OBD=30°,
∴PE=![]() PF,
PF,
∴![]() ,
,
设P坐标为(m,![]() ),(
),(![]() ),
),
则点F的坐标为(![]() ,
,![]() ),
),
∴PF=m-(![]() )=
)=![]() =
=![]() ,
,
∴当m=![]() 时,PF的最大值=
时,PF的最大值=![]() ,此时,
,此时,![]() 的最大值=
的最大值=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
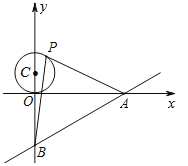
【题目】如图,已知直线![]() 与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
与x轴、y轴分别交于A、B两点,P是以C(0,1)为圆心,1为半径的圆上一动点,连结PA、PB.则△PAB面积的最大值是( )
A.8B.12C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
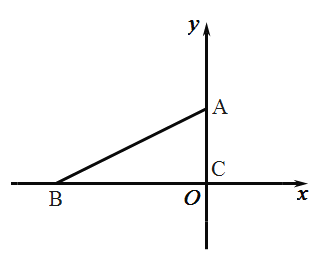
【题目】在![]() 纸片中,
纸片中,![]() ,
,![]() ,
,![]() .如图,直角顶点
.如图,直角顶点![]() 在原点,点
在原点,点![]() 在
在![]() 轴负半轴上,当点
轴负半轴上,当点![]() 在
在![]() 轴上向上移动时,点
轴上向上移动时,点![]() 也随之在
也随之在![]() 轴上向右移动,当点
轴上向右移动,当点![]() 到达原点时,点
到达原点时,点![]() 停止移动.在移动过程中,点
停止移动.在移动过程中,点![]() 到原点的最大距离是__________.
到原点的最大距离是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B![]() 90°,AB
90°,AB![]() 4,BC
4,BC![]() 2,以AC为边作△ACE,∠ACE
2,以AC为边作△ACE,∠ACE![]() 90°,AC=CE,延长BC至点D,使CD
90°,AC=CE,延长BC至点D,使CD![]() 5,连接DE.求证:△ABC∽△CED.
5,连接DE.求证:△ABC∽△CED.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是弦,D是弧BC的中点,过点D作EF垂直于直线AC,垂足为F,交AB的延长线于点E.
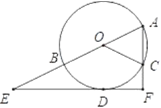
(1)求证:EF是⊙O的切线;
(2)若AF=6,EF=8,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AD=4,AB=2.点E是AB的中点,点F是BC边上的任意一点(不与B、C重合),△EBF沿EF翻折,点B落在B'处,当DB'的长度最小时,BF的长度为________.
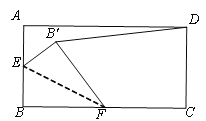
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:甲、乙两车分别从相距300km的A,B两地同时出发相向而行,甲到B地后立即返回,下图是它们离各自出发地的距离y与行驶时间x之间的函数图象.
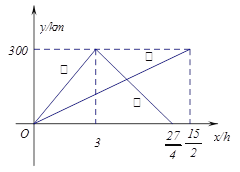
(1)求甲车离出发地的距离y与行驶时间x之间的函数关系式,并标明自变量![]() 的取值范围;
的取值范围;
(2)若已知乙车行驶的速度是40千米/小时,求出发后多长时间,两车离各自出发地的距离相等;
(3)它们在行驶过程中有几次相遇.并求出每次相遇的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
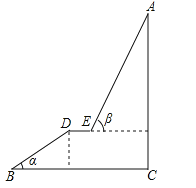
【题目】如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(参考数据:sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com