
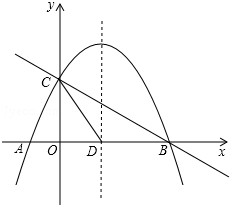
 ��ͼ��������y=-x2+mx+n��x�ύ��A��B���㣬y���ύ�ڵ�C�������ߵĶԳ��ύx���ڵ�D����֪A��-1��0����C��0��3��
��ͼ��������y=-x2+mx+n��x�ύ��A��B���㣬y���ύ�ڵ�C�������ߵĶԳ��ύx���ڵ�D����֪A��-1��0����C��0��3������ ��1���ɴ���ϵ����������Ԫһ�η��������m��n��ֵ���ɣ�
��2����ͼ1�У��������������ۢٵ�PD=DCʱ����CP=CDʱ���ֱ�д����P���꼴�ɣ�
��3�������BC�Ľ���ʽ�������E�ĺ�����Ϊa�����ı���CDBF�����=S��BCD+S��CEF+S��BEF���S��a�Ĺ�ϵʽ���ɶ��κ��������ʾͿ���������ۣ�
��� �⣺��1����������y=-$\frac{1}{2}$x2+mx+n����A��-1��0����C��0��2����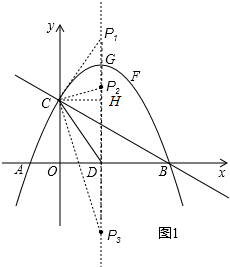
��ã�$\left\{\begin{array}{l}{m=\frac{3}{2}}\\{n=2}\end{array}\right.$��
�������ߵĽ���ʽΪ��y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2��
��2����ͼ1����y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2��
��y=-$\frac{1}{2}$��x-$\frac{3}{2}$��2+$\frac{25}{8}$��
�������ߵĶԳ�����ֱ��x=$\frac{3}{2}$��
��OD=$\frac{3}{2}$��
��C��0��3����
��OC=23
��Rt��OCD�У��ɹ��ɶ�������CD=$\frac{5}{3}$��
�ߡ�CDP����CDΪ���ĵ��������Σ�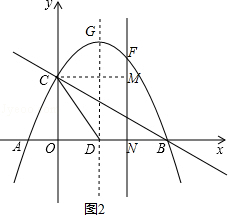
��CP1=DP2=DP3��
��CH��x����H��
��HP1=HD=2��
��DP1=4��
��P1��$\frac{3}{2}$��4����P2��$\frac{3}{2}$��$\frac{5}{3}$����P3��$\frac{3}{2}$��-$\frac{5}{3}$����
��3����y=0ʱ��0=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2
��x1=-1��x2=4��
��B��4��0����
��ֱ��BC�Ľ���ʽΪy=kx+b����ͼ��
$\left\{\begin{array}{l}{2=b}\\{0=4k+b}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=2}\end{array}\right.$��
��ֱ��BC�Ľ���ʽΪ��y=-$\frac{1}{2}$x+2��
��ͼ2������C��CM��EF��M����E��a��-$\frac{1}{2}$a+2����F��a��-$\frac{1}{2}$a2+$\frac{3}{2}$a+2����
��EF=-$\frac{1}{2}$a2+$\frac{3}{2}$a+2-��-$\frac{1}{2}$a+2��=-$\frac{1}{2}$a2+2a��0��x��4����
��S�ı���CDBF=S��BCD+S��CEF+S��BEF=$\frac{1}{2}$BD•OC+$\frac{1}{2}$EF•CM+$\frac{1}{2}$EF•BN��
=$\frac{1}{2}��\frac{5}{2}$��2+$\frac{1}{2}$a��-$\frac{1}{2}$a2+2a��+$\frac{1}{2}$��4-a����-$\frac{1}{2}$a2+2a����
=-a2+4a+$\frac{5}{2}$��0��x��4����
=-��a-2��2+$\frac{13}{2}$
��a=2ʱ��S�ı���CDBF��������=$\frac{13}{2}$��
��E��2��1����
���� �����Ƕ��κ����ۺ��⣬��Ҫ�����˴���ϵ������һ�κ����Ľ���ʽ�����ã����κ����Ľ���ʽ�����ã����ɶ��������ã����������ε����ʵ����ã��ı��ε���������ã����ʱ��������Ľ���ʽ�ǹؼ���


 ABC����ȫ�ž�ϵ�д�
ABC����ȫ�ž�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC�У�AB=AC����D�DZ�AB��һ�㣬��AD��DB=1��2��cot��DCB=$\sqrt{2}$��CD=4$\sqrt{3}$��
��ͼ����ABC�У�AB=AC����D�DZ�AB��һ�㣬��AD��DB=1��2��cot��DCB=$\sqrt{2}$��CD=4$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У�ADΪ��BAC��ƽ���ߣ�DE��AB��E��DF��AC��F����ABC�����56cm2��AB=20cm��AC=8cm����DE�ij���
��ͼ���ڡ�ABC�У�ADΪ��BAC��ƽ���ߣ�DE��AB��E��DF��AC��F����ABC�����56cm2��AB=20cm��AC=8cm����DE�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
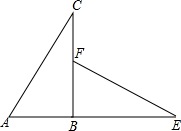 ��ͼ����ABC��ֱ�������Σ��ӳ�AB����E��ʹBE=BC����BC��ȡһ��F��ʹBF=AB������EF����ABC��ת�������FBE�غϣ���ش�
��ͼ����ABC��ֱ�������Σ��ӳ�AB����E��ʹBE=BC����BC��ȡһ��F��ʹBF=AB������EF����ABC��ת�������FBE�غϣ���ش��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 4�� | B�� | 3�� | C�� | 2�� | D�� | 1�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com