
分析 (1)首先求出CD、OE的长度各是多少;然后根据三角形的面积公式,求出S△ACD、S△ODE的值各是多少即可.
(2)首先判断出CD∥EF,即可推得△OCD∽OEF;然后根据$\frac{OD}{OF}=\frac{1}{2}$,可得S△OEF=4S△OCD,再根据S矩形ABCD=4S△OCD,即可推得S矩形ABCD=S△OEF.
(3)①首先延长OC到点E,使CE=AO,延长OD到点F,使DF=BO,连接EF,然后求出三角形OEF的面积,即可求出四边形ABCD的面积是多少.
②延长OD到点G,使DG=AO,延长OC到点H,使CH=FO,连接GH,然后求出三角形OGH的面积,即可求出六边形ABCDEF的面积是多少,进而判断出S与$\sqrt{3}$的关系即可.
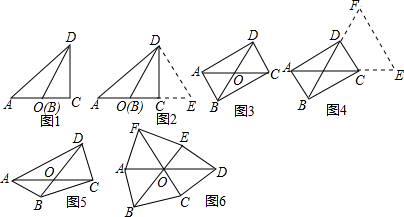
解答 解:(1)如图1,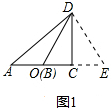 ,
,
∵BD=2,∠DOC=60°,
∴CD=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∵CE=AO,
∴OE=AC=2,
∴S△ACD=$\frac{1}{2}AC•CD=\frac{1}{2}×2×\sqrt{3}=\sqrt{3}$,
∴S△ODE=$\frac{1}{2}OE•CD$=$\frac{1}{2}×2×\sqrt{3}=\sqrt{3}$,
∴S△ACD=S△ODE=$\sqrt{3}$.
(2)如图2,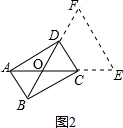 ,
,
∵点O是矩形ABCD的对角线的交点,
∴AO=CO,BO=DO,
又∵CE=AO,DF=BO,
∴CE=CO,DF=DO,
∴$\frac{DO}{DF}=\frac{CO}{CE}=1$,
∴CD∥EF,
∴△OCD∽OEF,
∵$\frac{OD}{OF}=\frac{1}{2}$,
∴S△OEF=4S△OCD,
又∵S矩形ABCD=4S△OCD,
∴S矩形ABCD=S△OEF.
(3)①如图3,延长OC到点E,使CE=AO,延长OD到点F,使DF=BO,连接EF,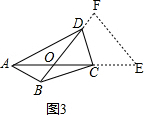 ,
,
∵CE=AO,AC=2,
∴OE=2,
∵DF=BO,BD=2,
∴OF=BD=2,
∵∠DOC=60°,
∴${S}_{四边形ABCD}{=S}_{△OEF}=\frac{1}{2}OF•OE•sin60°$=$\frac{1}{2}×2×2×\frac{\sqrt{3}}{2}=\sqrt{3}$,
即四边形ABCD的面积是$\sqrt{3}$.
②如图4,延长OD到点G,使DG=AO,延长OC到点H,使CH=FO,连接GH,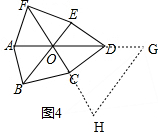 ,
,
∵DG=AO,AD=2,
∴OG=AD=2,
∵CH=FO,CF=2,
∴OH=CF=2,
∵∠DOC=∠AOF=60°,
∴S△OAB+S△OCD+S△OEF=S=${S}_{△OGH}=\frac{1}{2}OG•OH•sin60°=\frac{1}{2}×2×2×sin60°$=$\frac{1}{2}×2×2×\frac{\sqrt{3}}{2}=\sqrt{3}$,
即S=$\sqrt{3}$.
点评 (1)此题主要考查了几何变换综合题,考查了分析推理能力,考查了数形结合思想的应用,要熟练掌握.
(2)此题还考查了三角形的面积的求法,以及相似三角形的判定和性质的应用,要熟练掌握.


科目:初中数学 来源: 题型:选择题
| A. | 44.8cm | B. | 42cm | C. | 52cm | D. | 54cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,抛物线y=-x2+4x+5与x轴交于A、B两点,与y轴交于点C.已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点.△PCM是以CM为底的等腰三角形,则点P的坐标为(2+$\sqrt{6}$,3);当a=$\frac{\sqrt{6}+1}{4}$时,四边形PMEF周长最小.
如图,抛物线y=-x2+4x+5与x轴交于A、B两点,与y轴交于点C.已知M(0,1),E(a,0),F(a+1,0),点P是第一象限内的抛物线上的动点.△PCM是以CM为底的等腰三角形,则点P的坐标为(2+$\sqrt{6}$,3);当a=$\frac{\sqrt{6}+1}{4}$时,四边形PMEF周长最小.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2$\sqrt{5}$×3$\sqrt{5}$=6×25=150 | B. | 2$\sqrt{5}$×3$\sqrt{5}$=6×5=30 | C. | 2$\sqrt{5}$×3$\sqrt{5}$=6$\sqrt{5}$ | D. | 2$\sqrt{5}$×3$\sqrt{5}$=5$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
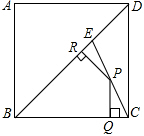 如图,E是边长为4的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BR于点R,则PQ+PR的值是( )
如图,E是边长为4的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BR于点R,则PQ+PR的值是( )| A. | 2$\sqrt{2}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | 2.9 | C. | 2.8 | D. | 2.7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com