
【题目】如图,点A1,A2在射线OA上,B1在射线OB上,依次作A2B2∥A1B1,A3B2∥A2B1,A3B3∥A2B2,A4B3∥A3B2,…. 若![]() 和
和![]() 的面积分别为1、9,则
的面积分别为1、9,则![]() 的面积是_________.
的面积是_________.

【答案】![]()
【解析】根据面积比等于相似比的平方,从而可推出相邻两个三角形的相似比为1:3,面积比为1:9,先利用等底三角形的面积之比等于高之比可求出第一个及第二个三角形的面积,再根据规律即可解决问题.
解:∵△A2B1B2和△A3B2B3的面积分别为1、9,A3B3∥A2B2,A3B2∥A2B1,
∴∠B1B2A2=∠B2B3A3,∠A2B1B2=∠A3B2B3,
∴△A2B1B2∽△A3B2B3,
∴![]() =
=![]() =
=![]() =
=![]() =
=![]() ,
,
∵A3B2∥A2B1,
∴△OA2B1∽△OA3B2,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴△OB1A2的面积为![]() ,△A1B1A2的面积为
,△A1B1A2的面积为![]() ,△A2B2A3的面积为3,△A3B3A4的面积为27,
,△A2B2A3的面积为3,△A3B3A4的面积为27,
∴△A1007B1007A1008`的面积为![]() ×32(n-1)=32n-3=32011,
×32(n-1)=32n-3=32011,
故答案为32011.
“点睛”此题考查了相似三角形的判定与性质即平行线的性质,解答本题的关键是掌握相似比等于面积比的平方,及平行线分线段成比例,难度较大,注意仔细观察图形,得出规律.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】在数学活动课上,同学们判断一个四边形门框是否为矩形.下面是某学习小组4位同学拟定的方案,其中正确的是
A. 测量对角线是否平分 B. 测量两组对边是否分别相等
C. 测量其中三个角是否是直角 D. 测量对角线是否相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABN中,∠B =90°,点M是AB上的动点(不与A,B两点重合),点C是BN延长线上的动点(不与点N重合),且AM=BC,CN=BM,连接CM与AN交于点P.
(1)在图1中依题意补全图形;


(2)小伟通过观察、实验,提出猜想:在点M,N运动的过程中,始终有∠APM=45°.小伟把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的一种思路:
要想解决这个问题,首先应想办法移动部分等线段构造全等三角形,证明线段相等,再构造平行四边形,证明线段相等,进而证明等腰直角三角形,出现45°的角,再通过平行四边形对边平行的性质,证明∠APM=45°.
他们的一种作法是:过点M在AB下方作MD![]() AB于点M,并且使MD=CN.通过证明△AMD
AB于点M,并且使MD=CN.通过证明△AMD![]() △CBM,得到AD=CM,再连接DN,证明四边形CMDN是平行四边形,得到DN=CM,进而证明△ADN是等腰直角三角形,得到∠DNA=45°.又由四边形CMDN是平行四边形,推得∠APM=45°.使问题得以解决.
△CBM,得到AD=CM,再连接DN,证明四边形CMDN是平行四边形,得到DN=CM,进而证明△ADN是等腰直角三角形,得到∠DNA=45°.又由四边形CMDN是平行四边形,推得∠APM=45°.使问题得以解决.
请你参考上面同学的思路,用另一种方法证明∠APM=45°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两组邻边分别相等的四边形叫做筝形.如图1,四边形ABCD是一个筝形,其中AD=CD,AB=CB,我们称这个四边形是“筝形ABCD”.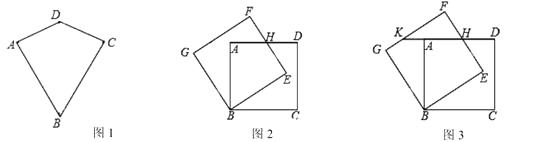
(1)根据筝形的定义判断下列命题是否正确,真命题打“√”,假命题打“×”.
①筝形有一组对角相等.
②菱形是筝形.
③筝形的面积为两条对角线长度的乘积.
(2)如图2,有一个公共顶点B的两个正方形ABCD与正方形BEFG全等,边AD与EF相交于点H.请你判断四边形BEHA是否是“筝形”,说明你的理由;
(3)如图3,当∠EBC=30°时,延长DA交GF于点K.若正方形ABCD边长为 ![]() ,求线段AK的长.
,求线段AK的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC、BD相交于点O,过点O作OE⊥BD交AD于点E.已知AB=2,△DOE的面积为 ![]() ,则AE的长为( )
,则AE的长为( ) 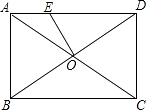
A.![]()
B.2
C.1.5
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com