
【题目】已知:如图,AB∥CD,

求:(1)在图(1)中∠B+∠D=?(2)在图(2)中∠B+∠E1+∠D=?(3)在图(3)中∠B+∠E1+∠E2+…+∠En﹣1+∠En+∠D=?
科目:初中数学 来源: 题型:
【题目】某水果商行计划购进A、B两种水果共200箱,这两种水果的进价、售价如下表所示:
价格 | 进价(元/箱) | 售价(元/箱) |
A | 60 | 70 |
B | 40 | 55 |
(1)若该商行进贷款为1万元,则两种水果各购进多少箱?
(2)若商行规定A种水果进货箱数不低于B种水果进货箱数的 ![]() ,应怎样进货才能使这批水果售完后商行获利最多?此时利润为多少?
,应怎样进货才能使这批水果售完后商行获利最多?此时利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图4所示,所有正方形的中心均在坐标原点,且每条边与x轴或y轴平行,从内到外,它们的边长依次为2,4,6,8 …,顶点依次用![]() …表示,则顶点A55的坐标是( ).
…表示,则顶点A55的坐标是( ).

A. (13,13) B. (-13,-13) C. (14,14) D. (-14,-14)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣ ![]() x2﹣3x﹣
x2﹣3x﹣ ![]() ,设自变量的值分别为x1 , x2 , x3 , 且﹣3<x1<x2<x3 , 则对应的函数值y1 , y2 , y3的大小关系是( )
,设自变量的值分别为x1 , x2 , x3 , 且﹣3<x1<x2<x3 , 则对应的函数值y1 , y2 , y3的大小关系是( )
A.y1>y2>y3
B.y1<y2<y3
C.y2>y3>y1
D.y2<y3<y1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角△ABC中,∠ACB=90°,∠B=60°,AD,CE分别是∠BAC和∠BCA的平分线,AD,CE相交于点F.
(1)求∠EFD的度数;
(2)判断FE与FD之间的数量关系,并证明你的结论.
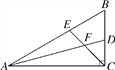
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线p:y=ax2+bx+c的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y=x2+2x+1和y=2x+2,则这条抛物线的解析式为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家到梧州市一茶厂购买茶叶,购买茶叶数量为x千克(x>0),总费用为y元,现有两种购买方式. 方式一:若商家赞助厂家建设费11500元,则所购茶叶价格为130元/千克;(总费用=赞助厂家建设费+购买茶叶费)
方式二:总费用y(元)与购买茶叶数量x(千克)满足下列关系式:y= ![]() .
.
请回答下面问题:
(1)写出购买方式一的y与x的函数关系式;
(2)如果购买茶叶超过150千克,说明选择哪种方式购买更省钱;
(3)甲商家采用方式一购买,乙商家采用方式二购买,两商家共购买茶叶400千克,总费用共计74600元,求乙商家购买茶叶多少千克?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com