
����Ŀ����ͼ��ʾ��ij���̶�����ɽ�£�ɽ����Ϊֱ��l������һ��·����Ҫ����ɽ�µ��¶ȣ���tan����ֵ������Ա��ɽ��P�������ƴ������ߣ��۲����ɽ���ϵ�һ���������������C������Ϊ31�㣬����B������Ϊ26.6�㣮��֪����BC=40�ף������ڵ�ɽ��OB=240�ף�OA=300�ף�ͼ�еĵ�O��B��C��A��P��ͬһƽ���ڣ���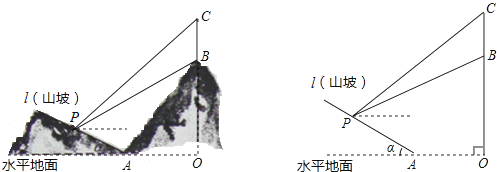
��1��P��OC�ľ��룮
��2��ɽ�µ��¶�tan����
�������sin26.6���0.45��tan26.6���0.50��sin31���0.52��tan31���0.60��
���𰸡�
��1��
�⣺��ͼ������P��PD��OC��D��PE��OA��E�����ı���ODPEΪ���Σ�
��Rt��PBD�У��ߡ�BDP=90�㣬��BPD=26.6�㣬
��BD=PDtan��BPD=PDtan26.6�㣻
��Rt��CPD�У��ߡ�CDP=90�㣬��CPD=31�㣬
��CD=PDtan��CPD=PDtan31�㣻
��CD��BD=BC��
��PDtan31�㩁PDtan26.6��=40��
��0.60PD��0.50PD=40��
���PD=400���ף���
��P��OC�ľ���Ϊ400��
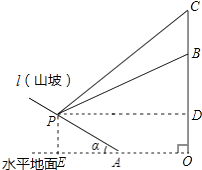
��2��
�⣺��Rt��PBD�У�BD=PDtan26.6���400��0.50=200���ף���
��OB=240�ף�
��PE=OD=OB��BD=40�ף�
��OE=PD=400�ף�
��AE=OE��OA=400��300=100���ף���
��tan��= ![]() =
= ![]() =0.4��
=0.4��
���¶�Ϊ0.4
����������1������P��PD��OC��D��PE��OA��E�����ı���ODPEΪ���Σ��Ƚ�Rt��PBD���ó�BD=PDtan26.6�㣻��Rt��CPD���ó�CD=PDtan31�㣻�ٸ���CD��BD=BC���г����̣����PD=400������õ�P��OC�ľ��룻��2��������õ��߶�PD�ij����PE=40��AE=100��Ȼ���ڡ�APE���������Ǻ����Ķ��弴����⣮


 ������ÿ�ʱ��ҵϵ�д�
������ÿ�ʱ��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ڳ�����ABCD����AB��12 cm��BC��6 cm.��P��AB�ߴӵ�A��ʼ���B��2 cm/s���ٶ��ƶ�����Q��DA�ߴӵ�D��ʼ���A��1 cm/s���ٶ��ƶ���
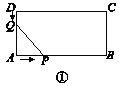
���P��Qͬʱ��������t(s)��ʾ�ƶ���ʱ�䣮
�����֣� DQ��________cm��AP��________cm.(�ú�t�Ĵ���ʽ��ʾ)
����չ��(1)��ͼ������t��________sʱ���߶�AQ���߶�AP��ȣ�
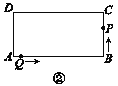
(2)��ͼ������P��Q�ֱ�B��A������˶�����P�����C��ֹͣ�˶���
��tΪ��ֵʱ��AQ��![]() CP?
CP?
��̽��������P��Q�ֱ��B��A���������A��B��C��D��A�ķ����˶�������P���Q��һ������ʱ����ֱ��д���������λ�ã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
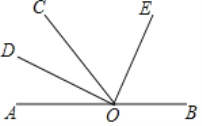
����Ŀ����ͼ��ʾ��OΪֱ��AB��һ�㣬ODƽ�֡�AOC����DOE=90�㣮
��1����AOD������� ______ ����COD������� ______
��2��OE�ǡ�BOC��ƽ��������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
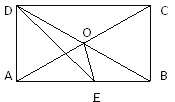
����Ŀ����ͼ���ھ���ABCD�У�DEƽ�֡�ADC�� �ҡ�EDO=15�������OED=________����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������г�����������ʾ��ͼ������ͼʾ�ش��������⣮
һ | �� | �� | �� | �� | �� | �� |
1 | 2 | 3 | 4 | 5 | ||
6 | 7 | 8 | 9 | 10 | 11 | 12 |
13 | 14 | 15 | 16 | 17 | 18 | 19 |
20 | 21 | 22 | 23 | 24 | 25 | 26 |
27 | 28 | 29 | 30 |
(1)��ͼ����һ���µ�������a��ʾ������ijһ����b��c��d�Ǹ���������3����b��c��d�ֱ���a�Ĺ�ϵ��b��________��c��________��d��________(�ú�a�Ĵ���ʽ���)��
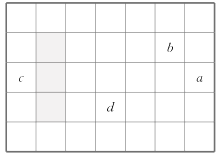
(2)��һ�������ο�Ȧ�������е�������(�� ͼ�е���Ӱ)������������֮�͵���51�������������ֱ��Ƕ��٣�
(3)����Ȧ�����������ĺͿ�����64��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����գ���ͼ������ֽ��ÿ��С�����εı߳���Ϊ1���ڷ���ֽ�ڽ���ABC����һ��ƽ�ƺ�õ���A��B��C����ͼ�б���˵�D�Ķ�Ӧ��D�䣮
��1��������������ƽ�ƺ����A��B��C����
��2���������������������AC���ϵĸ�BE��������������е������㣻
��3����A��B��C�������Ϊ ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
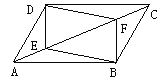
����Ŀ����ͼ����ABCD�У���E��F�ڶԽ���AC�ϣ���AE=CF����֤���ı���BEDF��ƽ���ı��Ρ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����C���߶�AB�ϣ�AC=8cm��CB=6cm����M��N�ֱ���AC��BC���е㣮
��1�����߶�MN�ij���
��2����CΪ�߶�AB����һ�㣬����AC+CB=a cm�������������䣬���ܲ���MN�ij����𣿲�˵�����ɣ�
��3����C���߶�AB���ӳ����ϣ�������AC��BC=b cm��M��N�ֱ�ΪAC��BC���е㣬���ܲ���MN�ij����𣿲�˵�����ɣ�
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC��AD��BC��CE��AB������ֱ�ΪD��E��AD��CE���ڵ�H����֪EH=EB=3��AE=4����CH�ij��ǣ� ��

A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com