
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),经过点
的左侧),经过点![]() 的直线
的直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与抛物线的另一个交点为
,与抛物线的另一个交点为![]() ,且
,且![]() .
.
![]() 直接写出点
直接写出点![]() 的坐标,并求直线
的坐标,并求直线![]() 的函数表达式(其中
的函数表达式(其中![]() ,
,![]() 用含
用含![]() 的式子表示);
的式子表示);
![]() 点
点![]() 是直线
是直线![]() 上方的抛物线上的一点,若
上方的抛物线上的一点,若![]() 的面积的最大值为
的面积的最大值为![]() ,求
,求![]() 的值;
的值;
![]() 设
设![]() 是抛物线对称轴上的一点,点
是抛物线对称轴上的一点,点![]() 在抛物线上,以点
在抛物线上,以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形能否成为矩形?若能,求出点
为顶点的四边形能否成为矩形?若能,求出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.
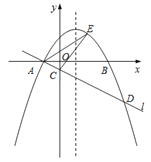
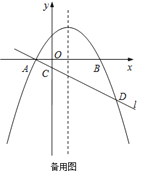
【答案】(1)A(﹣1,0),![]() ;(2)a=﹣
;(2)a=﹣![]() ;(3)
;(3)![]() 点的坐标为
点的坐标为![]() ,
,![]() .
.
【解析】
(1)解方程即可得到结论;根据直线l:y=kx+b过A(﹣1,0),得到直线l:y=kx+k,解方程得到点D的横坐标为4,求得k=a,得到直线l的函数表达式为y=ax+a;
(2)过E作EF∥y轴交直线l于F,设E(x,ax2﹣2ax﹣3a),得到F(x,ax+a),求出EF=ax2﹣3ax﹣4a,根据三角形的面积公式列方程即可得到结论;
(3)令ax2﹣2ax﹣3a=ax+a,即ax2﹣3ax﹣4a=0,得到D(4,5a),设P(1,m),①若AD是矩形ADPQ的一条边,②若AD是矩形APDQ的对角线,列方程即可得到结论.
(1)当y=0时,ax2﹣2ax﹣3a=0,解得:x1=﹣1,x2=3,∴A(﹣1,0),B(3,0).
∵直线l:y=kx+b过A(﹣1,0),∴0=﹣k+b,即k=b,∴直线l:y=kx+k.
∵抛物线与直线l交于点A,D,∴ax2﹣2ax﹣3a=kx+k,即ax2﹣(2a+k)x﹣3a﹣k=0.
∵CD=4AC,∴点D的横坐标为4,∴﹣3﹣![]() =﹣1×4,∴k=a,∴直线l的函数表达式为y=ax+a;
=﹣1×4,∴k=a,∴直线l的函数表达式为y=ax+a;
(2)过E作EF∥y轴交直线l于F,设E(x,ax2﹣2ax﹣3a),则F(x,ax+a),EF=ax2﹣2ax﹣3a﹣ax﹣a=ax2﹣3ax﹣4a,∴S△ACE=S△AFE﹣S△CEF=![]() (ax2﹣3ax﹣4a)(x+1)﹣
(ax2﹣3ax﹣4a)(x+1)﹣![]() (ax2﹣3ax﹣4a)x=
(ax2﹣3ax﹣4a)x=![]() (ax2﹣3ax﹣4a)=
(ax2﹣3ax﹣4a)=![]() a(x﹣
a(x﹣![]() )2﹣
)2﹣![]() a,∴△ACE的面积的最大值=﹣
a,∴△ACE的面积的最大值=﹣![]() a.
a.
∵△ACE的面积的最大值为![]() ,∴﹣
,∴﹣![]() a=
a=![]() ,解得:a=﹣
,解得:a=﹣![]() ;
;
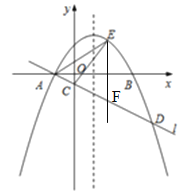
(3)以点A、D、P、Q为顶点的四边形能成为矩形,令ax2﹣2ax﹣3a=ax+a,即ax2﹣3ax﹣4a=0,解得:x1=﹣1,x2=4,∴D(4,5a).
∵抛物线的对称轴为直线x=1,设P(1,m),∴分两种情况讨论:
①若AD是矩形ADPQ的一条边,则易得Q(﹣4,21a),m=21a+5a=26a,则P(1,26a).
∵四边形ADPQ是矩形,∴∠ADP=90°,∴AD2+PD2=AP2,∴52+(5a)2+32+(26a﹣5a)2=22+(26a)2,即a2=![]() .
.
∵a<0,∴a=![]() ,∴P(1,
,∴P(1,![]() );
);
②若AD是矩形APDQ的对角线,则易得Q(2,﹣3a),m=5a﹣(﹣3a)=8a,则P(1,8a).
∵四边形APDQ是矩形,∴∠APD=90°,∴AP2+PD2=AD2,∴(﹣1﹣1)2+(8a)2+(1﹣4)2+(8a﹣5a)2=52+(5a)2,即a2=![]() .
.
∵a<0,∴a=﹣![]() ,∴P(1,﹣4).
,∴P(1,﹣4).
综上所述:点A、D、P、Q为顶点的四边形能成为矩形,点P(1,﹣![]() )或(1,﹣4).
)或(1,﹣4).


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的动点,将
上的动点,将![]() 沿
沿![]() 折叠.
折叠.
(1)当点![]() 与点
与点![]() 重合时,如图1.若
重合时,如图1.若![]() ,
,![]() ,则
,则![]() 的周长为_____.
的周长为_____.
(2)定义:若在三角形中,期中一条边是另一条边的2倍,则称这个三角形为“倍边三角形”.当点![]() 与点
与点![]() 重合时,如图2.若
重合时,如图2.若![]() ,则
,则![]() 是倍边三角形吗?请说明理由.
是倍边三角形吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AD⊥BC于D,将AB边沿AD折叠,发现B点的对应点E正好在AC的垂直平分线上,则∠C=_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角形三角板如图 1 所示放置,图 2 是由它抽像出的几何图形,B, C, E在同一 条直线上,连结DC.

(1)请找出图 2 中的全等三角形,并给予证明(说明:结论中不得含有未标识的字 母);
(2)证明:DC ⊥ BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() .图象的顶点为
.图象的顶点为![]() ,其图象与
,其图象与![]() 轴的交点
轴的交点![]() 、
、![]() 的横坐标分别为
的横坐标分别为![]() 、
、![]() ,与
,与![]() 轴负半轴交于点
轴负半轴交于点![]() .下面五个结论:①
.下面五个结论:①![]() ;②
;②![]() ;③当
;③当![]() 时,
时,![]() 随
随![]() 值的增大而增大;④当
值的增大而增大;④当![]() 时,
时,![]() ;⑤只有当
;⑤只有当![]() 时,
时,![]() 是等腰直角三角形.那么,其中正确的结论______.(只填你认为正确结论的序号)
是等腰直角三角形.那么,其中正确的结论______.(只填你认为正确结论的序号)
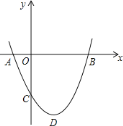
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在 Rt ![]() 中,
中,![]() ,
, ![]() ,点
,点 ![]() 为射线
为射线 ![]() 上一点,连接
上一点,连接 ![]() ,过点
,过点 ![]() 作线段
作线段 ![]() 的垂线
的垂线 ![]() ,在直线
,在直线 ![]() 上,分别在点
上,分别在点 ![]() 的两侧截取与线段
的两侧截取与线段 ![]() 相等的线段
相等的线段 ![]() 和
和 ![]() ,连接
,连接 ![]() ,
,![]() .
.
(1)当点 ![]() 在线段
在线段 ![]() 上时(点
上时(点 ![]() 不与点
不与点 ![]() ,
,![]() 重合),如图1,
重合),如图1,
①请你将图形补充完整;
②线段 ![]() ,
,![]() 所在直线的位置关系为 ,线段
所在直线的位置关系为 ,线段 ![]() ,
,![]() 的数量关系为 ;
的数量关系为 ;

(2)当点 ![]() 在线段
在线段 ![]() 的延长线上时,如图2,
的延长线上时,如图2,
①请你将图形补充完整;
②在(1)中②问的结论是否仍然成立?如果成立请进行证明,如果不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于任何数a,符号[a]表示不大于a的最大整数.
例如:[5.7]=5,[5]=5,[﹣1.5]=﹣2.
(1)[﹣![]() ]= ;
]= ;
(2)如果[a]=3,那么a的取值范围是 ;
(3)如果[![]() ]=﹣3,求满足条件的所有整数x.
]=﹣3,求满足条件的所有整数x.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读)如图1,四边形OABC中,OA=a,OC=3,BC=2,
∠AOC=∠BCO=90°,经过点O的直线l将四边形分成两部分,直线l与OC所成的角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处,我们把这个操作过程记为FZ[θ,a].
(理解)
若点D与点A重合,则这个操作过程为FZ[45°,3];
(尝试)
(1)若点D恰为AB的中点(如图2),求θ;
(2)经过FZ[45°,a]操作,点B落在点E处,若点E在四边形OABC的边AB上,求出a的值;若点E落在四边形OABC的外部,直接写出a的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com