解:(1)令y=0,则2x+4=0,
解得x=-2,
令x=0,则y=4,
所以,点A(-2,0)、D(0,4);
代入抛物线y=-

x
2+bx+c中,得:
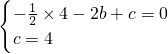
,解得
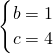
∴抛物线的解析式:y=-

x
2+x+4;
令y=0,得:0=-

x
2+x+4,解得 x
1=-2、x
2=4
∴点B(4,0).
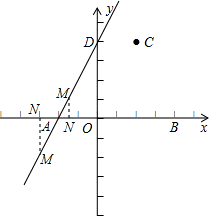
(2)∵S
△AOM:S
△OMD=1:3,∴AM:MD=1:3;
过点M作MN⊥x轴于N,如右图;
①当点M在线段AD上时,AM:AD=1:4;
∵MN∥OD,∴△AMN∽△ADO
∴MN=

OD=1、AN=

OA=

、ON=OA-AN=2-

=

;
∴M(-

,1);
②当点M在线段DA的延长线上时,AM:AD=1:2;
∵MN∥OD,∴△AMN∽△ADO
∴MN=

OD=2、AN=

OA=1、ON=OA+AN=3;
∴M(-3,-2);
综上,符合条件的点M有两个,坐标为:(-

,1)、(-3,-2).
(3)当x=2时,y=-

x
2+x+4=4,∴点C(2,4);
设点P的坐标为(0,m)(m>0),则有:
CP
2=m
2-8m+20、BP
2=m
2+16、BC
2=20;
①当CP=BP时,m
2-8m+20=m
2+16,解得 m=

;
②当CP=BC时,m
2-8m+20=20,解得 m
1=0(舍)、m
2=8(舍去);
③当BP=BC时,m
2+16=20,解得 m
1=-2(舍)、m
2=2;
综上,存在符合条件的点P,坐标为(0,

)或(0,2).
分析:(1)首先由已知的直线解析式确定点A、D的坐标,再利用待定系数法可求出抛物线的解析式,在抛物线的解析式中,令y=0,即可求出点B的坐标.
(2)△AOM、△OMD中,它们的高都可视作点O到直线AD的距离,所以它们的面积比可转化为底边的比,即AM:MD=1:3,显然MD>AM,所以只需考虑点M在线段AD上以及点M在线段DA的延长线上这两种情况,可过点M作x轴的垂线,通过构建相似三角形来求出点M的坐标.
(3)先求出点C的坐标,在知道了点C、B的坐标后,设出点P的坐标,然后表示出△BCP的三边长,分①CP=BP、②CP=BC、③BP=BC三种情况,列等式求出点P的坐标,需要注意的是要利用点P在y轴正半轴上,将不合题意的解舍掉.
点评:此题主要考查的是函数解析式的确定、三角形面积的解法、相似三角形以及等腰三角形的判定和性质等重要知识;后两题涉及的情况较多,都要进行分类讨论,以免出现漏解的情况.最后一题还要注意点P的位置,这是容易出错的地方.

 已知直线y=2x+4与x轴、y轴分别交于A,D两点,抛物线y=-
已知直线y=2x+4与x轴、y轴分别交于A,D两点,抛物线y=- x2+bx+c经过点A,D,点B是抛物线与x轴的另一个交点.
x2+bx+c经过点A,D,点B是抛物线与x轴的另一个交点. x2+bx+c中,得:
x2+bx+c中,得: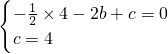 ,解得
,解得 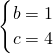
 x2+x+4;
x2+x+4; x2+x+4,解得 x1=-2、x2=4
x2+x+4,解得 x1=-2、x2=4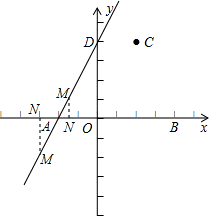 (2)∵S△AOM:S△OMD=1:3,∴AM:MD=1:3;
(2)∵S△AOM:S△OMD=1:3,∴AM:MD=1:3; OD=1、AN=
OD=1、AN= OA=
OA= 、ON=OA-AN=2-
、ON=OA-AN=2- =
= ;
; ,1);
,1); OD=2、AN=
OD=2、AN= OA=1、ON=OA+AN=3;
OA=1、ON=OA+AN=3; ,1)、(-3,-2).
,1)、(-3,-2). x2+x+4=4,∴点C(2,4);
x2+x+4=4,∴点C(2,4); ;
; )或(0,2).
)或(0,2).

 阅读快车系列答案
阅读快车系列答案