
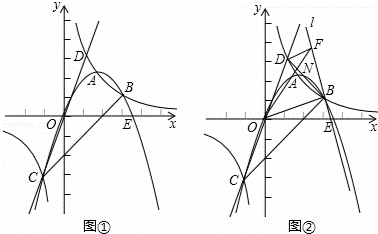
如图①,双曲线y=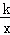 (k≠0)和抛物线y=ax2+bx(a≠0)交于A、B、C三点,其中B(3,1),C(﹣1,﹣3),直线CO交双曲线于另一点D,抛物线与x轴交于另一点E.
(k≠0)和抛物线y=ax2+bx(a≠0)交于A、B、C三点,其中B(3,1),C(﹣1,﹣3),直线CO交双曲线于另一点D,抛物线与x轴交于另一点E.
(1)求双曲线和抛物线的解析式;
(2)抛物线在第一象限部分是否存在点P,使得∠POE+∠BCD=90°?若存在,请求出满足条件的点P的坐标;若不存在,请说明理由;
(3)如图②过B作直线l⊥OB,过点D作DF⊥l于点F,BD与OF交于点N,求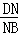 的值.
的值.
解:(1)∵抛物线y=ax2+bx(a≠0)过B(3,1),C(﹣1,﹣3),
∴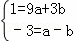 ,
,
解得: ,
,
∴抛物线的解析式为:y=﹣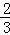 x2+
x2+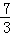 x,
x,
把B(3,1)代入y= (k≠0)得:1=
(k≠0)得:1=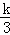 ,
,
解得:k=3,
∴双曲线的解析式为:y=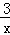 .
.
(2)∵B(3,1),C(﹣1,﹣3),设直线BC为y=kx+b,
∴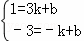 ,
,
解得k=1,b=﹣2,
∴直线BC为:y=x﹣2,
∴与坐标轴的交点(2,0),(0,﹣2),
过O作OM⊥BC,则OM=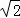 ,
,
∵B(3,1),C(﹣1,﹣3),
∴OB=OC=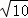 ,
,
∴BM=2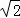 ,
,
∴tan∠COM=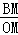 =
=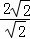 =2,
=2,
∵∠COM+∠BCD=90°,∠POE+∠BCD=90°,
∴∠POE=∠COM,
∴tan∠POE=2,
∵P点是抛物线上的点,设P(m,﹣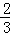 m2+
m2+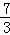 m),
m),
∴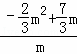 =2,
=2,
解得:m=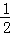 ,
,
∴P(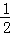 ,1),
,1),
(3)∵直线CO过C(﹣1,﹣3),
∴直线CO的解析式为y=3x,
解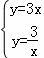 ,
,
解得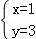 ,
,
∴D(1,3),
∵B(3,1),
∴直线OB的斜率=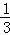 ,
,
∵直线l⊥OB,过点D作DF⊥l于点F,
∴DF∥OB,
∴直线l的斜率=﹣3,直线DF的斜率=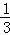 ,
,
∵直线l过B(3,1),直线DF过D(1,3),
∴直线l的解析式为y=﹣3x+10,直线DF解析式为y=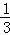 x+
x+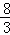 ,
,
解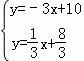 ,
,
解得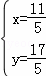 ,
,
∴F( ,
,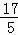 ),
),
∴DF=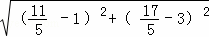 =
=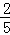
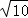 ,
,
∵DF∥OB,OB=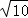 ,
,
∴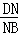 =
=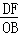 =
=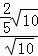 =
=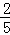 .
.


科目:初中数学 来源: 题型:
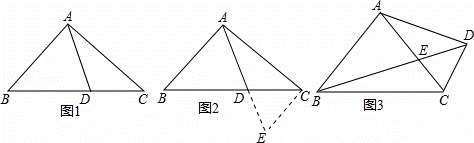
阅读下面材料:小腾遇到这样一个问题:如图1,在△ABC中,点D在线段BC上,∠BAD=75°,∠CAD=30°,AD=2,BD=2DC,求AC的长.
小腾发现,过点C作CE∥AB,交AD的延长线于点E,通过构造△ACE,经过推理和计算能够使问题得到解决(如图 2).
请回答:∠ACE的度数为 ,AC的长为 .
参考小腾思考问题的方法,解决问题:
如图 3,在四边形 ABCD中,∠BAC=90°,∠CAD=30°,∠ADC=75°,AC与BD交于点E,AE=2,BE=2ED,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com