
 研究几何图形,我们往往先给出这类图形的定义,再研究它的性质和判定方法.我们给出如下定义:如图,四边形ABCD中,AB=AD,CB=CD像这样两组邻边分别相等的四边形叫做“筝形”;
研究几何图形,我们往往先给出这类图形的定义,再研究它的性质和判定方法.我们给出如下定义:如图,四边形ABCD中,AB=AD,CB=CD像这样两组邻边分别相等的四边形叫做“筝形”;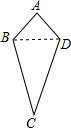
分析 (1)菱形四边相等,根据筝形定义可得菱形是特殊的“筝形”;
(2)①连结BD,根据等边对等角可得∠ABD=∠ADB,∠DBC=∠BDC,进而可得∠ABC=∠ADC;
②连接AC,BD,根据线段垂直平分线的判定可得AC是BD的垂直平分线,根据等腰三角形三线合一的性质可得AC平分∠BAC和∠BCD;
③根据线段垂直平分线的性质可得如果AC是BD的垂直平分线,则AB=AD,BC=CD.
解答 证明:(1)正确,
∵菱形四边相等,
∴菱形是特殊的“筝形”;
(2)①连结BD,在△ABD和△BCD中,
∵AB=AD,BC=CD,
∴∠ABD=∠ADB,∠DBC=∠BDC
∴∠ABC=∠ADC;
②“筝形”有一条对角线平分一组对角(答案不唯一),
连接AC,BD,
∵AB=AD,
∴A在BD的垂直平分线上,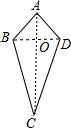
∵BC=DC,
∴C在BD的垂直平分线上,
∴AC是BD的垂直平分线,
∵AB=AD,BC=CD,
∴AC平分∠BAC和∠BCD,
∴“筝形”有一条对角线平分一组对角,
故答案为:“筝形”有一条对角线平分一组对角;
③有一条对角线垂直平分另一条对角线的四边形是筝形(答案不唯一).
故答案为:有一条对角线垂直平分另一条对角线的四边形是筝形.
点评 此题主要考查了四边形的综合,关键是掌握等腰三角形的性质,以及等腰三角形的判定:等边对等角.到线段两端点距离相等的点在线段的垂直平分线上.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:解答题
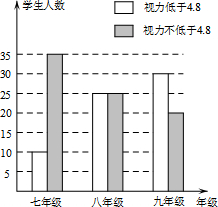 在学习了“普查与抽样调查”之后,某校八(1)班数学兴趣小组对该校学生的视力情况进行了抽样调查,并画出了如图所示的条形统计图.请根据图中信息解决下列问题:
在学习了“普查与抽样调查”之后,某校八(1)班数学兴趣小组对该校学生的视力情况进行了抽样调查,并画出了如图所示的条形统计图.请根据图中信息解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
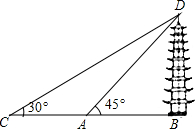 五一节,某校数学兴趣小组的同学相约去东台西溪“海春轩塔”参观,并测量其高度.如图,塔身BD与地面垂直,他们先在A处测得塔顶端点D的仰角为45°,再沿着BA的方向后退16cm至C处,测得塔顶端点D的仰角为30°,求“海春轩塔”BD的高度.($\sqrt{3}$≈1.73,结果保留一位小数)
五一节,某校数学兴趣小组的同学相约去东台西溪“海春轩塔”参观,并测量其高度.如图,塔身BD与地面垂直,他们先在A处测得塔顶端点D的仰角为45°,再沿着BA的方向后退16cm至C处,测得塔顶端点D的仰角为30°,求“海春轩塔”BD的高度.($\sqrt{3}$≈1.73,结果保留一位小数)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
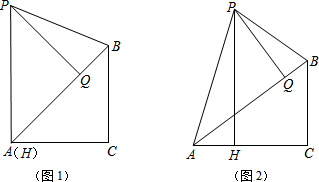
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
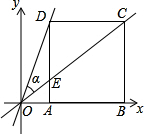 边长为2的正方形ABCD在平面直角坐标系中如图放置,已知点A的横坐标为1,作直线OC与边AD交于点E.
边长为2的正方形ABCD在平面直角坐标系中如图放置,已知点A的横坐标为1,作直线OC与边AD交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
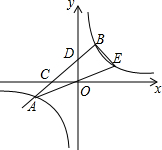 如图,直线AB与双曲线交于点A,B,与x轴,y轴分别交于点C,D,与x轴的夹角α满足tanα=$\frac{3}{4}$,且OD=6,CD:CB=1:2.
如图,直线AB与双曲线交于点A,B,与x轴,y轴分别交于点C,D,与x轴的夹角α满足tanα=$\frac{3}{4}$,且OD=6,CD:CB=1:2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com