
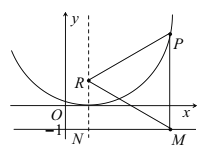
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌOЮЊзјБъдЕуЃЌЕуAзјБъЮЊЃЈЉ2![]() ЃЌ0ЃЉЃЌЁЯOAB=90ЁуЃЌЁЯAOB=30ЁуЃЌНЋЁїOABШЦЕуOАДЫГЪБеыЗНЯђа§зЊЃЌа§зЊНЧЮЊІСЃЈ0ЁуЃМІСЁм150ЁуЃЉЃЌдка§зЊЙ§ГЬжаЃЌЕуAЁЂBЕФЖдгІЕуЗжБ№ЮЊЕуAЁфЁЂBЁфЃЎ
ЃЌ0ЃЉЃЌЁЯOAB=90ЁуЃЌЁЯAOB=30ЁуЃЌНЋЁїOABШЦЕуOАДЫГЪБеыЗНЯђа§зЊЃЌа§зЊНЧЮЊІСЃЈ0ЁуЃМІСЁм150ЁуЃЉЃЌдка§зЊЙ§ГЬжаЃЌЕуAЁЂBЕФЖдгІЕуЗжБ№ЮЊЕуAЁфЁЂBЁфЃЎ
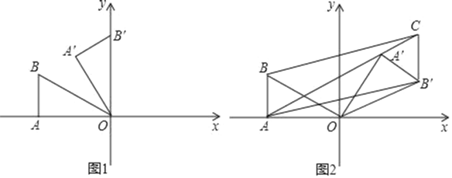
ЃЈ1ЃЉШчЭМ1ЃЌЕБІС=60ЁуЪБЃЌжБНгаДГіЕуAЁфЁЁ ЁЁЁЂBЁфЁЁ ЁЁЕФзјБъЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌЕБІС=135ЁуЪБЃЌЙ§ЕуBЁфзїABЕФЦНааЯпНЛAAЁфбгГЄЯпгкЕуCЃЌСЌНгBCЃЌABЁфЃЎ
ЂйХаЖЯЫФБпаЮABЁфCBЕФаЮзДЃЌВЂЫЕУїРэгЩЃЌ
ЂкЧѓДЫЪБЕуAЁфКЭЕуBЁфЕФзјБъЃЛ
ЃЈ3ЃЉЕБІСгЩ30Ёуа§зЊЕН150ЁуЪБЃЌЃЈ2ЃЉжаЕФЯпЖЮBЁфCвВЫцжЎвЦЖЏЃЌЧыЧѓГіBЁфCЫљЩЈЙ§ЕФЧјгђЕФУцЛ§ЃПЃЈжБНгаДГіНсЙћМДПЩЃЉЃЎ
ЁОД№АИЁПЃЈ1ЃЉЃЈЉ![]() ЃЌ3ЃЉЃЌЃЈ0ЃЌ4ЃЉЃЛЃЈ2ЃЉЂйЫФБпаЮABЁфCBЪЧЦНааЫФБпаЮЃЌЯъМћНтЮіЃЛЂкAЁфЃЈ
ЃЌ3ЃЉЃЌЃЈ0ЃЌ4ЃЉЃЛЃЈ2ЃЉЂйЫФБпаЮABЁфCBЪЧЦНааЫФБпаЮЃЌЯъМћНтЮіЃЛЂкAЁфЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌЕуBЁфЃЈ
ЃЉЃЌЕуBЁфЃЈ![]() +
+![]() ЃЌ
ЃЌ![]() Љ
Љ![]() ЃЉЃЛЃЈ3ЃЉ12
ЃЉЃЛЃЈ3ЃЉ12
ЁОНтЮіЁП
ЃЈ1ЃЉШчЭМ1жаЃЌзїAЁфEЁЭOBЁфгкEЃЎНтжБНЧШ§НЧаЮЧѓГіEOЃЌAЁфEМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉЂйШчЭМ2жаЃЌНсТлЃКЫФБпаЮABЁфCBЪЧЦНааЫФБпаЮЃЎжЛвЊжЄУїBЁфCЁЮABЃЌBЁфC=ABЃЛ
ЂкЙ§ЕуAЁфзїAЁфEЁЭxжсгкEЃЎЙ§ЕуBЁфзїBЁфFЁЭAЁфEгкFЃЌНтжБНЧШ§НЧаЮЧѓГіOEЁЂEFЁЂBЁфFМДПЩЃЛ
ЃЈ3ЃЉBЁфCЩЈЙ§ЕФУцЛ§=SЦНааЫФБпаЮBЁфBЁхCЁхCЁфЃЌгЩДЫМЦЫуМДПЩЃЛ
НтЃКЃЈ1ЃЉШчЭМ1жаЃЌзїAЁфEЁЭOBЁфгкEЃЎ
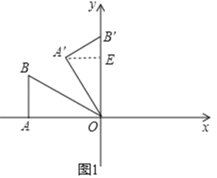
дкRtЁфЁїOAЁфBЁфжаЃЌЁпЁЯAЁфOBЁф=30ЁуЃЌOAЁф=2![]() ЃЌ
ЃЌ
Ёрcos30Ёу=![]() ЃЌ
ЃЌ
ЁрOBЁф=4ЃЌ
ЁрBЁфЃЈ0ЃЌ4ЃЉЃЌ
дкRtЁїOAЁфEжаЃЌЁпOAЁф=2![]() ЃЌ
ЃЌ
ЁрAЁфE=![]() ЃЌOE=
ЃЌOE=![]() AЁфE=3ЃЌ
AЁфE=3ЃЌ
ЁрAЁфЃЈЉ![]() ЃЌ3ЃЉЃЎ
ЃЌ3ЃЉЃЎ
ЙЪД№АИЮЊЃЈЉ![]() ЃЌ3ЃЉЃЌЃЈ0ЃЌ4ЃЉЃЎ
ЃЌ3ЃЉЃЌЃЈ0ЃЌ4ЃЉЃЎ
ЃЈ2ЃЉЂйШчЭМ2жаЃЌНсТлЃКЫФБпаЮABЁфCBЪЧЦНааЫФБпаЮЃЎ
РэгЩЃКЁпBЁфCЁЮABЃЌ
ЁрЁЯBЁфCA=ЁЯBACЃЌ
ЁпЁЯBAC+ЁЯCAO=90ЁуЃЌ
ЁрЁЯBЁфCAЁф+ЁЯCAO=90ЁуЃЌ
гжЁпЁЯBЁфAЁфC+ЁЯOAЁфA=90ЁуЃЌЧва§зЊЕУЕНOA=OAЁфЃЌдђЁЯCAO=ЁЯOAЁфAЃЌ
ЁрЁЯBЁфCAЁф=ЁЯBЁфAЁфCЃЌ
ЁрBЁфC=BЁфAЁфЃЌ
гжЁпAЁфBЁф=ABЃЌ
ЁрBЁфC=ABЃЌ
ЁрЫФБпаЮABЁфCBЪЧЦНааЫФБпаЮЃЎ
ЂкЙ§ЕуAЁфзїAЁфEЁЭxжсгкEЃЎ
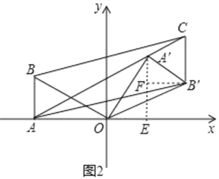
гЩAЃЈЉ2![]() ЃЌ0ЃЉЃЌПЩЕУOA=2
ЃЌ0ЃЉЃЌПЩЕУOA=2![]() ЃЌ
ЃЌ
гжЁпЁЯOAB=90ЁуЃЌЁЯAOB=30ЁуЃЌ
ЁрAB=2ЃЌOB=4ЃЌдђOAЁф=2![]() ЃЌAЁфBЁф=2ЃЌ
ЃЌAЁфBЁф=2ЃЌ
гЩЁЯAOAЁф=135ЁуЃЌЕУЕНЁЯAЁфOE=45ЁуЃЌ
ЁрOE=AЁфE=![]() OAЁф=
OAЁф=![]() ЃЌ
ЃЌ
ЁрЕуAЁфЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
Й§ЕуBЁфзїBЁфFЁЭAЁфEгкFЃЌ
гЩЁЯEAЁфO=45ЁуЃЌЕУЁЯEAЁфBЁф=45ЁуЃЌ
ЁрBЁфF=AЁфF=![]() ЁС2=
ЁС2=![]() ЃЌ
ЃЌ
ЁрEF=![]() Љ
Љ![]() ЃЌOE+BЁфF=
ЃЌOE+BЁфF=![]() +
+![]() ЃЌ
ЃЌ
ЁрЕуBЁфЃЈ![]() +
+![]() ЃЌ
ЃЌ![]() Љ
Љ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ3ЃЉШчЭМ3жаЃЌНсКЯЃЈ2ЃЉжЊЃК
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
![]() ЩЯЕФИпЮЊ
ЩЯЕФИпЮЊ![]()
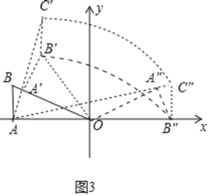
BЁфCЩЈЙ§ЕФУцЛ§=SЦНааЫФБпаЮBЁфBЁхCЁхCЁф=6ЁС2=12ЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊе§ЗНаЮABCDЕФБпГЄЮЊ3ЃЌEЁЂFЗжБ№ЪЧABЁЂBCБпЩЯЕФЕуЃЌЧвЁЯEDF=45ЁуЃЌНЋЁїDAEШЦЕуDФцЪБеыа§зЊ90ЁуЃЌЕУЕНЁїDCMЃЎШєAE=1ЃЌдђFMЕФГЄЮЊ ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§y=kx+bЕФЭМЯѓгыЗДБШР§КЏЪ§y=![]() ЃЈxЃО0ЃЉЕФЭМЯѓНЛгкAЃЈ2ЃЌЉ1ЃЉЁЂBЃЈ
ЃЈxЃО0ЃЉЕФЭМЯѓНЛгкAЃЈ2ЃЌЉ1ЃЉЁЂBЃЈ![]() ЃЌnЃЉСНЕуЃЎжБЯпy=2гыyжсНЛгкЕуCЃЎ
ЃЌnЃЉСНЕуЃЎжБЯпy=2гыyжсНЛгкЕуCЃЎ
1ЃЉЧѓвЛДЮКЏЪ§гыЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
2ЃЉЧѓЁїABCЕФУцЛ§ЃЛ
3ЃЉжБНгаДГіВЛЕШЪНkx+bЃО![]() дкШчЭМЫљЪОЗЖЮЇФкЕФНтМЏЃЎ
дкШчЭМЫљЪОЗЖЮЇФкЕФНтМЏЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЗўзАЙЋЫОЪдЯњвЛжжГЩБОЮЊУПМў50дЊЕФ![]() аєЩРЃЎЪдЯњжаЗЂЯжЃЌЕБЯњЪлЕЅМлЪЧ60дЊЪБЃЌЪлГі400МўЃЛЯњЪлЕЅМлУПНЕЕЭ1дЊЃЌЖрЪлГі10МўЃЎЩшЪдЯњжаЯњЪлЕЅМл
аєЩРЃЎЪдЯњжаЗЂЯжЃЌЕБЯњЪлЕЅМлЪЧ60дЊЪБЃЌЪлГі400МўЃЛЯњЪлЕЅМлУПНЕЕЭ1дЊЃЌЖрЪлГі10МўЃЎЩшЪдЯњжаЯњЪлЕЅМл![]() ЃЈдЊЃЉЪБЕФЯњЪлСПЮЊ
ЃЈдЊЃЉЪБЕФЯњЪлСПЮЊ![]() ЃЈМўЃЉЃЎ
ЃЈМўЃЉЃЎ
ЃЈ1ЃЉЧѓ![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЩшИУЙЋЫОЛёЕУЕФзмРћШѓЮЊ![]() дЊЃЌЧѓ
дЊЃЌЧѓ![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ3ЃЉШєвЊЯњСПВЛЕЭгк200МўЃЌЧвЛёРћжСЩй5250дЊЃЌдђЪлМлгІдкКЮЗЖЮЇФкЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ![]() ЪЧХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌ
ЪЧХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌ![]() ЪЧХзЮяЯпЖдГЦжсЩЯЕФвЛЕуЃЎ
ЪЧХзЮяЯпЖдГЦжсЩЯЕФвЛЕуЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФЖЅЕуМАгы![]() жсНЛЕуЕФзјБъЃЛ
жсНЛЕуЕФзјБъЃЛ
ЃЈ2ЃЉ![]() ЪЧЙ§Еу
ЪЧЙ§Еу![]() ЧвЦНаагк
ЧвЦНаагк![]() жсЕФжБЯпЃЌ
жсЕФжБЯпЃЌ![]() гыХзЮяЯпЕФЖдГЦжсЕФНЛЕуЮЊ
гыХзЮяЯпЕФЖдГЦжсЕФНЛЕуЮЊ![]() ЃЌ
ЃЌ![]() ЃЌДЙзуЮЊЕу
ЃЌДЙзуЮЊЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЂйЕБ![]() ЪЧЕШБпШ§НЧаЮЪБЃЌЧѓ
ЪЧЕШБпШ§НЧаЮЪБЃЌЧѓ![]() ЕуЕФзјБъЃЛ
ЕуЕФзјБъЃЛ
ЂкЧѓжЄЃК![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПОиаЮжНЦЌABCDЃЌAB=7ЃЌBC=4ЃЌдкОиаЮБпЩЯгавЛЕуPЃЌЧвDP=3ЃЎНЋОиаЮжНЦЌелЕўЃЌЪЙЕуBгыЕуPжиКЯЃЌелКлЫљдкжБЯпНЛОиаЮСНБпгкЕуEЁЂFЃЌдђEF=__________________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуAдкЯпЖЮBDЩЯЃЌдкBDЕФЭЌВрзїЕШбќRtЁїABCКЭЕШбќRtЁїADEЃЌЦфжаЁЯABC=ЁЯAED=90ЁуЃЌCDгыBEЁЂAEЗжБ№НЛгкЕуPЁЂMЃЎЖдгкЯТСаНсТлЃКЂйЁїCAMЁзЁїDEMЃЛЂкCD=2BEЃЛЂлMPMD=MAMEЃЛЂм2CB2=CPCMЃЎЦфжае§ШЗЕФЪЧЃЈЁЁЁЁЃЉ

A. ЂйЂкB. ЂйЂкЂлC. ЂйЂкЂлЂмD. ЂйЂлЂм
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕШбќЁїABCШчЭМЗХжУЃЌЖЅНЧЕФЖЅЕуCдкжБЯпmЩЯЃЌЗжБ№Й§ЕуAЁЂBзїжБЯпmЕФДЙЯпЃЌДЙзуЗжБ№ЮЊEЁЂDЃЌЧвAEЃНCDЃЎ
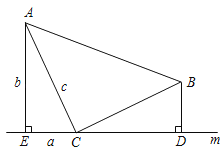
ЃЈ1ЃЉЧѓжЄЃКЁїAECЁеЁїCDBЃЛ
ЃЈ2ЃЉШєЩшЁїAECЕФШ§БпГЄЗжeЮЊaЁЂbЁЂcЃЌРћгУДЫЭМжЄУїЙДЙЩЖЈРэЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдЫГЧнХЦбОЦВњгкЩНЮїдЋЧњ.мьЦбШїдЖдкККДњОЭвбУћдыОЦЬГЃЌЮЊРњДњЕлЭѕНЋЯрЫљЯВАЎЃЌВЂБЛСаЮЊРњДњгљЩХЯуѕВ.нХЦбОЦдкЪаГЁЕФЯњЪлСПЛсИљОнМлИёЕФБфЛЏЖјБфЛЏ.нХЦбОЦУПЦПЕФГЩБОМлЪЧ![]() дЊЃЌФГГЌЪаНЋЪлМлЖЈЮЊ
дЊЃЌФГГЌЪаНЋЪлМлЖЈЮЊ![]() дЊЪБЃЌУПЬьПЩвдЯњЪл
дЊЪБЃЌУПЬьПЩвдЯњЪл![]() ЦПЃЌШєЪлМлУПНЕЕЭ
ЦПЃЌШєЪлМлУПНЕЕЭ![]() дЊЃЌУПЬьМДПЩЖрЯњЪл
дЊЃЌУПЬьМДПЩЖрЯњЪл![]() ЦП(ЪлМлВЛФмИпгк
ЦП(ЪлМлВЛФмИпгк![]() дЊ)ЃЌШєЩшУПЦПНЕМл
дЊ)ЃЌШєЩшУПЦПНЕМл![]() дЊ
дЊ
![]() гУКЌ
гУКЌ![]() ЕФДњЪ§ЪНБэЪОнХЦбОЦУПЬьЕФЯњЪлСП.
ЕФДњЪ§ЪНБэЪОнХЦбОЦУПЬьЕФЯњЪлСП.
![]() УПЦПнХЦбОЦЕФЪлМлЖЈЮЊЖрЩйдЊЪБУПЬьЛёШЁЕФРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйЃП
УПЦПнХЦбОЦЕФЪлМлЖЈЮЊЖрЩйдЊЪБУПЬьЛёШЁЕФРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com