
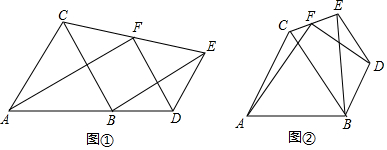
 如图①,△ABC为等边三角形,D为AB延长线上一点,BD=DE.∠BDE=120°,连接EB、EC,F为EC的中点,连接FA、FD.
如图①,△ABC为等边三角形,D为AB延长线上一点,BD=DE.∠BDE=120°,连接EB、EC,F为EC的中点,连接FA、FD.分析 (1)方法一:利用倍长中线法得出△CFM≌△EFD,进而得出FM=FD,再判断出AM=AD,最后利用等腰三角形的三线合一即可即可得出结论;
方法二:先判断出∠CBE=90°,再利用直角三角形斜边的中线等于斜边的一半,得出BF=EF=CF,进而判断出△BDF≌△EDF,△ABF≌△ACF,最后代换即可得出结论.
(2)利用倍长中线法得出△CFM≌△EFD,即CM=DE,由旋转的性质进而判断出点M,C,B在同一条直线上,进而判断出△ACM≌△ABD,即可同(1)的方法得出结论;
(3)同(2)的方法得出CM=BD,∠MCF=∠DEF再用周角的定义,三角形的内角和得出∠ACM=∠ABD,即可判断出△ACM≌△ABD,最后同(2)的方法得出结论.
解答 解:(1)方法一:如图 ①,延长AC,DF相交于点M,
①,延长AC,DF相交于点M,
∵△ABC为等边三角形,∴
AC=AB,∠BAC=60°,
∵∠BDE=120°,
∴DE∥AC,
∴∠M=∠EDF,
∵点F是CE中点,
∴CF=EF,
在△CFM和△EFD中,$\left\{\begin{array}{l}{∠M=∠EDF}\\{∠CFM=∠EFD}\\{CF=EF}\end{array}\right.$,
∴△CFM≌△EFD,
∴FM=FD,CM=DE,
∵BD=DE,
∴BD=CM.
∴AC+CM=AB+BD,
∴AM=AD,
∵FM=FD,
∴∠DAF=∠CAF=$\frac{1}{2}$∠BAC=30°,AF⊥DF,
∴AF=$\sqrt{3}$DF,
方法二,如图, 连接BF,
连接BF,
∵∠BDE=120°,BD=DE,
∴∠DBE=30°,
∵∠ABC=60°,
∴∠CBE=90°,
∵点F是CE中点,
∴BF=EF=CF,
在△BDF和△EDF中,$\left\{\begin{array}{l}{BD=DE}\\{DF=DF}\\{BF=EF}\end{array}\right.$,
∴△BDF≌△EDF,
∴∠BFD=∠EFD,
同理:△ABF≌△ACF,
∴∠BAF=∠CAF=$\frac{1}{2}$∠BAC=30°,∠AFB=∠AFC,
∵∠AFD+∠AFC+∠EFD=180°,
∴∠AFD=90°,
在Rt△AFD中,∠DAF=30°,
∴AF=$\sqrt{3}$DF,
故答案为:AF⊥DF,AF=$\sqrt{3}$DF;
(2)(1)的结论仍然成立,
理由:如图②, 延长DF至M使FM=FD,连接CM,AM,
延长DF至M使FM=FD,连接CM,AM,
∵点F是CE中点,
∴CF=EF,
在△MCF和△DEF中,$\left\{\begin{array}{l}{CF=EF}\\{∠CFM=∠EFD}\\{FM=FD}\end{array}\right.$,
∴△MCF≌△DEF,
∴CM=DE,
∵BD=DE,
∴CM=BD,
由旋转知,∠CBD=60°,
∵BD=DE.∠BDE=120°,
∴∠BED=∠EBD=30°,
∴∠CBE=30°=∠BED,
∴DE∥BC,
∴∠BCE+∠CED=180°,
∵△MCF≌△DEF,
∴∠FCM=∠FED,
∴∠FCM+∠BCE=180°,
∴点M,C,B在同一条直线上,
∵∠ACB=60°,
∴∠ACM=120°
在△ACM和△ABD中,$\left\{\begin{array}{l}{AC=AB}\\{∠ACM=∠ABD=120°}\\{CM=BD}\end{array}\right.$,
∴△ACM≌△ABD,
∴∠CAM=∠BAD,AM=AD,
∵FM=FD,
∴AF⊥DF,
∵∠BAC=60°,
∴∠BAD+∠DAF+∠CAF=60°,
∴∠DAF+∠MAC+∠CAF=2∠DAF=60°,
∴∠DAF=30°,
∴AF=$\sqrt{3}$DF,
即:AF⊥DF,AF=$\sqrt{3}$DF,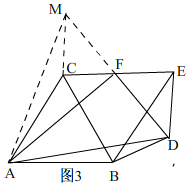
(3)(1)的结论仍然成立,
理由:如图3,延长DF至M使FM=FD,连接CM,AM,
∵点F是CE中点,
∴CF=EF,
在△MCF和△DEF中,$\left\{\begin{array}{l}{CF=EF}\\{∠CFM=∠EFD}\\{FM=FD}\end{array}\right.$,
∴△MCF≌△DEF,
∴∠MCF=∠DEF,CM=DE,
∵BD=DE,
∴CM=BD,
∵∠ABD=∠ABC+∠CBE+∠DBE=90°+∠CBE,
∵∠ACM=360°-∠MCF-∠ACB-∠BCE
=360°-∠DEF-60°-∠BCE
=300°-∠DEF-∠BCE
=300°-(∠BED+∠BEC)-∠BCE
=300°-(30°+∠BEC)-∠BCE
=270°-(∠BCE+∠BEC)
=270°-(180°-∠CBE)
=90°+∠CBE,
∴∠ACM=∠ABD,
在△ACM和△ABD中,$\left\{\begin{array}{l}{AC=AB}\\{∠ACM=∠ABD}\\{CM=BD}\end{array}\right.$,
∴△ACM≌△ABD,
∴∠CAM=∠BAD,AM=AD,
∵FM=FD,
∴AF⊥DF,
∵∠BAC=60°,
∴∠BAD+∠DAF+∠CAF=60°
∴∠DAF+∠MAC+∠CAF=2∠DAF=60°,
∴∠DAF=30°,
∴AF=$\sqrt{3}$DF,
即:AF⊥DF,AF=$\sqrt{3}$DF.
点评 此题是几何变换综合题,主要考查了直角三角形斜边的中线等于斜边的一半,含30°的直角三角形的性质,等边三角形的性质,全等三角形的判定和性质,周角的定义,垂直的方法的判定,利用倍长中线法构造全等三角形是解本题的关键,(3)判断出∠ACM=∠ABD是解本题的难点,属于中考压轴题.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:选择题
 将一列整数1,2,3,-4,-5,-6,7,-8,-9,-10,…按如图所示排列.如第一个顶峰的数是-6,第二个峰顶的数是15,那么第2016个峰顶的数是( )
将一列整数1,2,3,-4,-5,-6,7,-8,-9,-10,…按如图所示排列.如第一个顶峰的数是-6,第二个峰顶的数是15,那么第2016个峰顶的数是( )| A. | 18150 | B. | -18150 | C. | 18141 | D. | -18141 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a+b}{2}$ | B. | $\frac{a+b}{11}$ | C. | $\frac{5a+6b}{11}$ | D. | $\frac{1}{2}$($\frac{a}{5}$+$\frac{b}{6}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
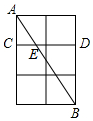 如图,在2×3的方格纸中,每个小正方形的边长均为1,点A,B,C,D都在格点上,AB与CD交于点E,则EB的长为$\frac{2\sqrt{13}}{3}$.
如图,在2×3的方格纸中,每个小正方形的边长均为1,点A,B,C,D都在格点上,AB与CD交于点E,则EB的长为$\frac{2\sqrt{13}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 飞机上升9000米,再上升-5000米,则飞机实际上升4000米 | |
| B. | 一个正数,一个负数,它们表示的意义一定相反 | |
| C. | 0是最小的有理数 | |
| D. | 正数和负数统称为有理数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com