练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．抛物线y=ax2-1上有一点P（2，2），平移该抛物线，使其顶点落在点A（0，1）处，这时，点P落在点Q处，则点Q的坐标为（2，4）．

    分析 先利用二次函数的性质得到抛物线y=ax2-1的顶点坐标为（0，-1），再利用顶点的坐标变换规律得到抛物线的平移规律，然后利用此平移规律写出点P平移到点Q时的坐标．

    解答 解：抛物线y=ax2-1的顶点坐标为（0，-1），
    ∵点（0，-1）向上平移2个单位得到点A（0，1），
    ∴点P（2，2）向上平移2个单位得到点Q（2，4）．
    故答案为（2，4）．

    点评 本题考查了二次函数图象与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

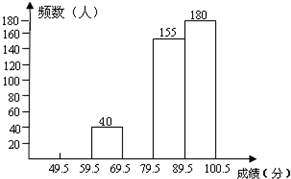    12．某区初中有10000名学生参加安全应急预案知识竞赛活动，为了了解本次知识竞赛的成绩分布情况，从中抽取了500名学生的得分（得分取正整数，满分100分）进行统计：
    频率分布表
    分  组频  数频  率
    49.5～59.525
    59.5～69.5400.08
    69.5～79.50.20
    79.5～89.5155
    89.5～100.51800.36
    合  计5001
    请你根据不完整的频率分布表．解答下列问题：
    （1）补全频率分布表；   
    （2）补全频数分布直方图；
    （3）若将得分转化为等级，规定得分低于59.5分评为“D”，59.5～69.5分评为“C”，69.5～89.5分评为“B”，89.5～100.5分评为“A”，估计这次10000名学生中约有多少人评为“D”？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    13．若（3x-5）2+|$\frac{1}{3}$y+$\frac{1}{5}$x|=0，则y2009=-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．为了解某校八年级学生的体育锻炼时间，小明随机调查了该年级40名同学一周内参加体育锻炼的情况，并把它绘制成条形统计图（如图）．
    （1）样本中参加体育锻炼时间的众数是10h，中位数是9h，平均数是9.1h；
    （2）若该校八年级共有400名学生，请估计该年级有多少名学生一周参加体育锻炼的时间不低于9h．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图1，抛物线y=ax2+bx-3与y轴于点，与x轴交于A、B两点，OB=3OA，∠ABC=45°
    （1）求此抛物线的解析式；
    （2）如图2，平移此抛物线使其顶点为坐标原点，点M为y轴上一动点，MN与抛物线只有唯一公共点N点，点G在x轴上，∠GNM=∠OMN，求证：直线NG必过一定点，并求此定点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．（1）计算   $-\sqrt{{{（-2）}^2}}+{\;}^3\sqrt{-8}+\sqrt{25}+|{1-\sqrt{3}}|$
    （2）解方程组$\left\{\begin{array}{l}{3（x+y）-2（2x-y）=3}\\{\frac{2（x-y）}{3}-\frac{x+y}{4}=-\frac{1}{12}}\end{array}\right.$
    （3）解不等式组$\left\{\begin{array}{l}{x-3（x-1）≤7}\\{1-\frac{2-5x}{3}＜x}\end{array}\right.$并把它的解集在数轴上表示出来．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．对于一元二次方程ax2+bx+c=0（a≠0）总有4a+2b+c=0，则方程一定有一个根为x=2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．若一个长方形的面积为x2-5xy+6y2，它的一条边长为x-2y，则它的周长为4x-10y．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．如图①：MA1∥NA2，图②：MA1∥NA3，图③：MA1∥NA4，图④：MA1∥NA5，…，则第n个图中的∠A1+∠A2+∠A3+…+∠An+1=180•n°（用含n的代数式表示）．

    查看答案和解析>>

    同步练习册答案