
【题目】按照题中提供的思路点拨,先填空,然后完成解答的全过程.
如图,已知AB=AD,∠BAD=60°,∠BCD=120°,延长BC,使CE=CD,连接DE,求证:BC+DC=AC.
思路点拨:(1)由已知条件AB=AD,∠BAD=60°,可知△ABD是_三角形.同理由已知条件∠BCD=120°得到∠DCE=_,且CE=CD,可知_;
(2)要证BC+DC=AC,可将问题转化为证两条线段相等,即_=_;
(3)要证(2)中所填写的两条线段相等,可以先证明_.请写出完整的证明过程.
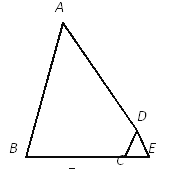
【答案】(1)等边,60°,△DCE是等边三角形;(2)AC,BE;(3)△BED≌△ACD,证明见解析.
【解析】试题分析:(1)连接BD,根据等边三角形判定推出即可;求出∠DCE=60°,得到等边三角形DCE即可;
(3)根据等边三角形性质推出AD=BD,CD=DE,∠ADB=∠CDE=60°,推出∠ADC=∠BDE,证△ADC≌△BDE即可;
(4)由(3)即可得出答案.
试题解析:(1)(1)解:连接BD,
∵AB=AD,∠BAD=60°,
∴△ABD是等边三角形,
∵∠BCD=120°,
∴∠DCE=180°-∠BCD=180°-120°=60°,
∵CE=CD,
∴△DCE是等边三角形,
故答案为:等边,60°,△DCE是等边三角形.
(2)证明:∵等边三角形ABD和DCE,
∴AD=BD,CD=DE,∠ADB=∠CDE=60°,
∴∠ADB+∠BDC=∠CDE+∠BDC,
即∠ADC=∠BDE,
在△ADC和△BDE中,
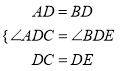
∴△ADC≌△BDE,
∴AC=BE=BC+CE,
故答案为:BE,AC.
(3)△BED≌△ACD
证明过程如下:连接AC,BD.
因为AB=AD,∠BAD=60°,所以△ABD是等边三角形.所以AD=BD,∠ADB=60°.
因为∠BCD=120°,所以∠DCE=180°-∠BCD=180°-120°=60°.
因为CE=CD,所以△DCE是等边三角形.所以CD=DE,∠CDE=60°.
所以∠ADB+∠BDC=∠CDE+∠BDC,即∠ADC=∠BDE.
在△ADC和△BDE中,AD=BD,∠ADC=∠BDE,DC=DE,所以△ADC≌△BDE.所以AC=BE=BC+CE=BC+DC.


科目:初中数学 来源: 题型:
【题目】有七张正面分别标有数字﹣3,﹣2,﹣1,0,1,2,3的卡片,它们除数字不同外其余全部相同.现将它们背面朝上,洗匀后从中随机抽取一张,记卡片上的数字为a,则使关于x的一元二次方程x2﹣2(a﹣1)x+a(a﹣3)=0有两个不相等的实数根,且以x为自变量的二次函数y=x2﹣(a2+1)x﹣a+2的图象不经过点(1,O)的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次机器人测试中,要求机器人从A出发到达B处.如图1,已知点A在O的正西方600cm处,B在O的正北方300cm处,且机器人在射线AO及其右侧(AO下方)区域的速度为20cm/秒,在射线AO的左侧(AO上方)区域的速度为10cm/秒. 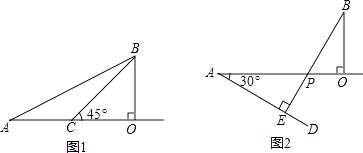
(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732,
≈1.732, ![]() ≈2.236,
≈2.236, ![]() ≈2.449)
≈2.449)
(1)分别求机器人沿A→O→B路线和沿A→B路线到达B处所用的时间(精确到秒);
(2)若∠OCB=45°,求机器人沿A→C→B路线到达B处所用的时间(精确到秒);
(3)如图2,作∠OAD=30°,再作BE⊥AD于E,交OA于P.试说明:从A出发到达B处,机器人沿A→P→B路线行进所用时间最短.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,BC=a,AC=b,AB=c,设c为最长边,当a2+b2=c2时,△ABC是直角三角形;当a2+b2≠c2时,利用代数式a2+b2和c2的大小关系,探究△ABC的形状(按角分类).
(1)当△ABC三边分别为6、8、9时,△ABC为 三角形;当△ABC三边分别为6、8、11时,△ABC为 三角形.
(2)猜想,当a2+b2 c2时,△ABC为锐角三角形;当a2+b2 c2时,△ABC为钝角三角形.
(3)判断当a=2,b=4时,△ABC的形状,并求出对应的c的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品50件.生产一件A产品需要甲种原料9千克,乙种原料3千克,可获利润700元;生产一件B产品,需要甲种原料4千克,乙种原料10千克,可获利润1200元.
(1)设生产x件A种产品,写出其题意x应满足的不等式组;
(2)由题意有哪几种按要求安排A、B两种产品的生产件数的生产方案?请您帮助设计出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】倡导健康生活,推进全民健身,某社区要购进A,B两种型号的健身器材若干套,A,B两种型号健身器材的购买单价分别为每套310元,460元,且每种型号健身器材必须整套购买.
(1)若购买A,B两种型号的健身器材共50套,且恰好支出20000元,求A,B两种型号健身器材各购买多少套?
(2)若购买A,B两种型号的健身器材共50套,且支出不超过18000元,求A种型号健身器材至少要购买多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,∠ACB=90°点E是AB的中点,连接CE,过点E作ED⊥BC于点D,在DE的延长线上取一点F,使AF=CE,求证四边形ACEF是平行四边形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com