
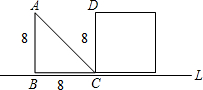
 AB与CD重合.设x秒时,三角形与正方形不重叠部分的面积为ym2.
AB与CD重合.设x秒时,三角形与正方形不重叠部分的面积为ym2.| 1 |
| 2 |
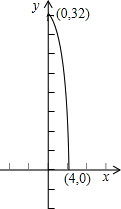
| 2 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
| ||
| 2 |
| ||
| 2 |
| 3 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 点为点E,将线段PE绕点P按顺时针方向旋转60°得PC.
点为点E,将线段PE绕点P按顺时针方向旋转60°得PC. | 7 |
| 2 |
| ||
| 2 |
| 7 |
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
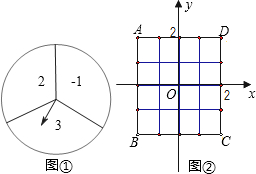 的数字为纵坐标).
的数字为纵坐标).| 2 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:2011-2012学年浙江省翠苑中学九年级下学期3月考数学卷(带解析) 题型:解答题
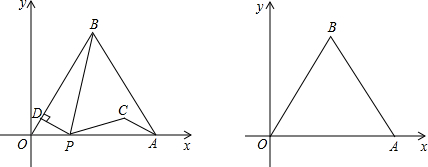
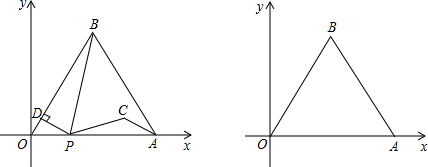
如图,边长为4的等边三角形AOB的顶点O在坐标原点,点A在x轴正半轴上,点B在第一象限.一动点P沿x轴以每秒1个单位长的速度向点A匀速运动,当点P到达点A时停止运动,设点P运动的时间是t秒.将线段BP的中点绕点P按顺时针方向旋转60°得点C,点C随点P的运动而运动,连接CP、CA,过点P作PD⊥OB于点D.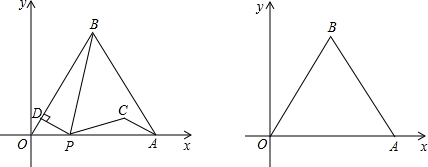
(1)填空:PD的长为 (用含t的代数式表示);
(2)求点C的坐标(用含t的代数式表示);
(3)在点P从O向A运动的过程中,△PCA能否成为直角三角形?若能,求t的值.若不能,请说明理由;
(4)填空:在点P从O向A运动的过程中,点C运动路线的长为
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com