
| A�� |  | B�� | 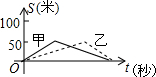 | ||
| C�� |  | D�� |  |
���� ���ݼ�����Ӿ�ٶȿ�Ѹ������50�ף�������Ӿ�ٶ����ȼ�����Ӿʱ�䳤���ɵô𰸣�
��� �⣺A��������Ӿ�ٶȿ�Ѹ������50�ף�������Ӿ�ٶ����ȼ�����Ӿʱ�䳤����A�������⣻
B��������Ӿ�ٶȿ�Ѹ������50�ף�������Ӿ�ٶ����ȼ�����Ӿʱ�䳤����B����
C����û���س����㣬��C����
D����û���س����㣬��D����
��ѡ��A��
���� ���⿼���˺���ͼ�����������ǽ���ؼ���������Ӿ�ٶȿ�Ѹ������50�ף�������Ӿ�ٶ����ȼ�����Ӿʱ�䳤���������ͬʱ���س����㣮


 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ����һöӲ�ң�Ӳ�����ʱ���泯��������¼� | |
| B�� | ��4����������������У�����һ��������������2�����DZ�Ȼ�¼� | |
| C�� | ��������꼶�²���ѧ�̿��飬������97ҳ������¼� | |
| D�� | ij�ֲ�Ʊ���н���Ϊ0.001������100�Ų�Ʊһ����1���н� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=��x-3��2 | B�� | y=��x+3��2 | C�� | y=x2-3 | D�� | y=x2+3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 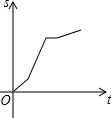 | B�� | 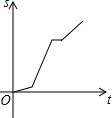 | C�� |  | D�� | 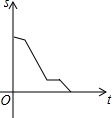 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
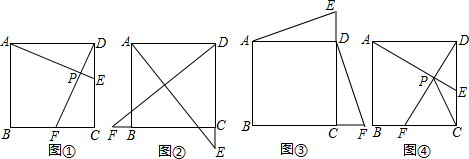
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ӡ��a����λ��ǧ�ᣩ | 1��a��5 | 5��a��10 |
| ��ɫ����λ��Ԫ/�ţ� | 2.2 | 2.0 |
| �ڰף���λ��Ԫ/�ţ� | 0.8 | 0.6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ֱ֪��y1=$\frac{1}{2}$x��˫����y2=$\frac{k}{x}$��k��0������A��B���㣬�ҵ�A�ĺ�����Ϊ4��
��ͼ����ֱ֪��y1=$\frac{1}{2}$x��˫����y2=$\frac{k}{x}$��k��0������A��B���㣬�ҵ�A�ĺ�����Ϊ4���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
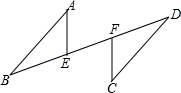 ��ͼ��AB��CD��AB=CD��E��F��BD�ϵ����㣬Ҫʹ��ABE�ա�CDF�����������µ��߶κ���ĸ���������ӵ�һ��������BE=DF���A=��C���AEB=��CFD��ֻдһ���������ɣ���
��ͼ��AB��CD��AB=CD��E��F��BD�ϵ����㣬Ҫʹ��ABE�ա�CDF�����������µ��߶κ���ĸ���������ӵ�һ��������BE=DF���A=��C���AEB=��CFD��ֻдһ���������ɣ����鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com