
如图,在□ ![]() 中,
中,![]() 是对角线
是对角线![]() 的中点,过点
的中点,过点![]() 作
作![]() 的垂线与边
的垂线与边![]() 、
、![]() 分别交于
分别交于![]() 、
、![]() ,求证:四边形
,求证:四边形![]() 是菱形.
是菱形.

科目:初中数学 来源:第2章《二次函数》中考题集(43):2.7 最大面积是多少(解析版) 题型:解答题
 所对的圆心角为120°,已知圆的半径为2cm,并建立如图所示的直角坐标系.
所对的圆心角为120°,已知圆的半径为2cm,并建立如图所示的直角坐标系.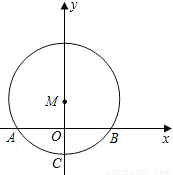
查看答案和解析>>
科目:初中数学 来源:第6章《二次函数》中考题集(47):6.4 二次函数的应用(解析版) 题型:解答题
 所对的圆心角为120°,已知圆的半径为2cm,并建立如图所示的直角坐标系.
所对的圆心角为120°,已知圆的半径为2cm,并建立如图所示的直角坐标系.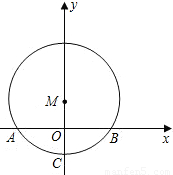
查看答案和解析>>
科目:初中数学 来源:2009年海南省琼海市中考数学模拟试卷(解析版) 题型:解答题
 所对的圆心角为120°,已知圆的半径为2cm,并建立如图所示的直角坐标系.
所对的圆心角为120°,已知圆的半径为2cm,并建立如图所示的直角坐标系.
查看答案和解析>>
科目:初中数学 来源:2006年甘肃省嘉峪关市中考数学试卷(课标卷)(解析版) 题型:解答题
 所对的圆心角为120°,已知圆的半径为2cm,并建立如图所示的直角坐标系.
所对的圆心角为120°,已知圆的半径为2cm,并建立如图所示的直角坐标系.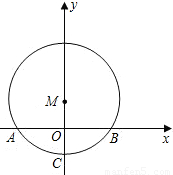
查看答案和解析>>
科目:初中数学 来源:2006年甘肃省武威市中考数学试卷(课标卷)(解析版) 题型:解答题
 所对的圆心角为120°,已知圆的半径为2cm,并建立如图所示的直角坐标系.
所对的圆心角为120°,已知圆的半径为2cm,并建立如图所示的直角坐标系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com