
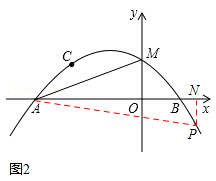
����Ŀ����ͼ��������![]() ��a��0��������A����3��0����B��1��0����C����2��1������y���ڵ�M��
��a��0��������A����3��0����B��1��0����C����2��1������y���ڵ�M��
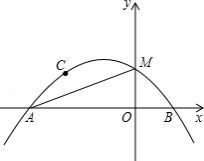
��1���������ߵı���ʽ��
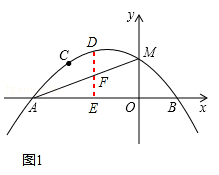
��2��DΪ�������ڵڶ��������ϵ�һ�㣬��DE��ֱx���ڵ�E�����߶�AM�ڵ�F�����߶�DF���ȵ����ֵ�������ʱ��D�����ꣻ
��3�����������Ƿ����һ��P����PN��ֱx���ڵ�N��ʹ���Ե�P��A��NΪ���������������MAO���ƣ������ڣ����P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��![]()
��2����D������Ϊ![]()
��3�����������ĵ�P������Ϊ����8����15������2��![]() ������10����39����
������10����39����
��������
��������1���ѵ�A��B��C������ֱ������֪�����ߵĽ���ʽ�г�����ϵ������Ԫһ�η����飬ͨ����÷����鼴�����ϵ����ֵ��
��2���ɣ�1���е������߽���ʽ�����M������Ϊ��0��1�����������ô���ϵ�����������ֱ��AM�Ĺ�ϵʽΪ![]() �����������D������Ϊ
�����������D������Ϊ![]() �����F������Ϊ
�����F������Ϊ![]() ������DF����
������DF����![]() �ĺ�������ʽ�����ݶ��κ�����ֵԭ�������߶�DF�����ֵ��
�ĺ�������ʽ�����ݶ��κ�����ֵԭ�������߶�DF�����ֵ��
��3���Ե�P��λ�ý��з������ۣ���P�ֱ�λ�ڵ�һ��������������������������������������εĶ�Ӧ�߳ɱ������н��
�⣺��1����A����3��0����B��1��0����C����2��1������![]() �ã�
�ã�
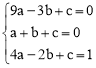 �����
�����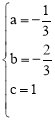 ��
��
�������ߵı���ʽΪ![]() ��
��
��2����x=0���������߱���ʽ����y=1������M������Ϊ��0��1����
��ֱ��MA�ı���ʽΪy=kx+b��
��![]() �����
�����![]() ��
��
��ֱ��MA�ı���ʽΪ![]() ��
��
���D������Ϊ![]() ��
��
���F������Ϊ![]() ��
��
��![]() ��
��
����![]() ʱ��DF�����ֵΪ
ʱ��DF�����ֵΪ![]() ��
��
��ʱ![]() ������D������Ϊ
������D������Ϊ![]() ��
��
��3�����ڵ�P��ʹ���Ե�P��A��NΪ���������������MAO���ơ�
��P![]() ��
��
��Rt��MAO�У�AO=3MO��Ҫʹ�������������ƣ��������֪����P�������ڵ�һ���ޡ�
�����P�ڵڶ�����ʱ������P��������ֱ��MN�ϣ���ֻ��PN=3NM��
��![]() ����
����![]() ��
��
���m=��3��m=��8��
����ʱ��3��m��0������ʱ���������ĵ㲻���ڡ�
������P�ڵ�������ʱ��
����P��������ֱ��MN�ϣ���ֻ��PN=3NM��
��![]() ����
����![]() ��
��
���m=��3����ȥ����m=��8��
��m=��8ʱ��![]() ������ʱ��P������Ϊ����8����15����
������ʱ��P������Ϊ����8����15����
������P�ڵ�������ʱ��
��AN=3PNʱ����![]() ��
��
��m2+m��6=0��
���m=��3����ȥ����m=2��
��m=2ʱ��![]() ��
��
����ʱ��P������Ϊ��2��![]() ����
����
��PN=3NA����![]() ����m2��7m��30=0��
����m2��7m��30=0��
���m=��3����ȥ����m=10��
��m=10ʱ��![]() ������ʱ��P������Ϊ��10����39����
������ʱ��P������Ϊ��10����39����
�������������������ĵ�P������Ϊ����8����15������2��![]() ������10����39����
������10����39����


 100�ִ�����ĩ���ϵ�д�
100�ִ�����ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ڵ����㳡��������ý���ע����������Ƶ��Ϊ�˽��й�ר�ñ�����Сƽ���˽ⱾС����������㳡�����Ŀ�����������һ�γ������飬�Ѿ�������㳡�����Ŀ�����Ϊ�ĸ���Σ�A �dz���ͬ��B ��ͬ��Ҫ��ʱ�����ƣ�C ����ν��D ����ͬ������������������ͼ1��ͼ2������������ͳ��ͼ��

�������ͼ���ṩ����Ϣ����������⣺
��1���α����ľ����ж����ˣ�
��2����ͼ1��ͼ2����������
��3����ͼ2����C������������ε�Բ�ĽǵĶ�����
��4�����Ƹ�С��4000�������ж����㳡�����Ŀ�����ʾ��ͬ������A��κ�B��Σ��Ĵ�Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��Ӧ������֯����ġ���̼����ĺ��٣��������������������������г��ϰ࣮��һ�죬���������г��Ӽ��ﵽ�����ϰ࣬;�������г��������ϣ���������һ��ʱ�䣬���ú�������У�ֱ�����﹤���������������г�������������ʻ����������ҵľ���![]() ���ף������ʱ��
���ף������ʱ��![]() �����ӣ��Ĺ�ϵ��ʾ����ͼ��
�����ӣ��Ĺ�ϵ��ʾ����ͼ��
��1�������Ӽҳ��������ֹ���ʱ���ٶ�Ϊ �ף����ӣ�
��2����������ʱ ���ӣ�
��3�����߶�BC����Ӧ�ĺ�����ϵʽ����Ҫ��д���Ա�����ȡֵ��Χ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��Լ�õ磬ijУ�ڱ�ѧ�ڳ��ƶ�����ϸ���õ�ƻ������ʵ��ÿ��ȼƻ�����2�ȵ磬��ô��ѧ�ڵ��õ������ᳬ��2 530�ȣ����ʵ��ÿ��ȼƻ���Լ2�ȵ磬��ô��ѧ�ڵ��õ����������2 200�ȣ�����ѧ�ڵ���Уʱ�䰴110����㣬��ôѧУÿ���õ���Ӧ������ʲô��Χ�ڣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���͵��϶���������һ�ֽ��͡��������¼���������ijƷ���͵��϶�����������ͨ��������سɱ����ݹ������±���
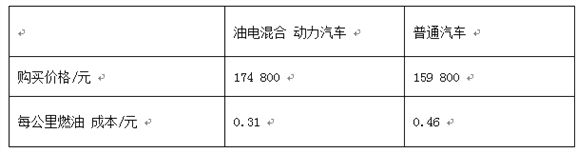
����ʦ�ƻ�����һ����Ʒ�Ƶ��͵��϶�����������ֻ���dz��ۺ�ȼ�ͳɱ�������£�����ʦԤ����δ��10����ó��ɱ�������10����ƽ��ÿ����ʻ����̴ﵽһ��������ʱ��ѡ���͵��϶��������ijɱ���������ͨ����������ʦԤ����10����ƽ��ÿ����ʻ�������������Ϊ���ٹ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ��ְ���ڻ����ҹۿ���ʮ�Ŵ�����Ļʽ��ÿ����13�ˣ�����1��������ÿ����14�ˣ����12����λ�����������ҹ�����λ��������__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ƽ��ֱ������ϵ�У���֪A��3��4����B��3����1����C����3����2����D����2��3��.
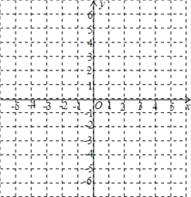
��1����ͼ�ϻ����ı���ABCD�������ı���ABCD�������
��2����PΪ�ı���ABCD����һ�㣬��֪P����Ϊ����1��1�������ı���ABCDͨ��ƽ�ƺ�P�������Ϊ��2����2��������ƽ�ƵĹ�����ֱ��д���ı���ABCDƽ�ƺ���ĸ���������꣮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com