
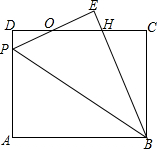
 如图,矩形ABCD中,P为AD边上一点,沿直线BP将△ABP翻折至△EBP(点A的对应点为点E),PE与CD相交于点O,且OE=OD.
如图,矩形ABCD中,P为AD边上一点,沿直线BP将△ABP翻折至△EBP(点A的对应点为点E),PE与CD相交于点O,且OE=OD.分析 (1)证明△DOP≌△EOH,根据全等三角形的对应边相等证得OP=OH,据此即可证得;
(2)设DP=x,则EH=x,BH=10-x,在Rt△BCH中利用勾股定理即可列方程求解.
解答 解:(1)证明:∵OD=OE,∠D=∠E=90°,∠DOP=∠EOH
∴△DOP≌△EOH,
∴OP=OH,
∴PO+OE=OH+OD,
∴PE=DH;
(2)设DP=x,则EH=x,BH=10-x,
CH=CD-DH=CD-PE=10-(8-x)=2+x,
∴在Rt△BCH中,BC2+CH2=BH2
(2+x)2+82=(10-x)2,
∴x=$\frac{4}{3}$
∴DP=$\frac{4}{3}$.
点评 本题考查了图象的折叠,以及勾股定理,在求线段的长时,常用的方法是转化为直角三角形中,利用勾股定理求解.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
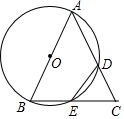 如图,在△ABC中,以AB为直径的⊙O分别交AC,BC于点D,E.连接ED,若ED=EC.
如图,在△ABC中,以AB为直径的⊙O分别交AC,BC于点D,E.连接ED,若ED=EC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a+1)(a-1)=a2-1 | B. | 3x2+6x=3x(x+2) | C. | x2-x+1=x(x-1)+1 | D. | a(x-y)=ax-ay |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
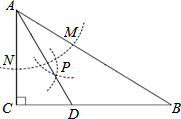 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列结论正确的有( )
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列结论正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com