
| A. | k>-3 | B. | k<5 | C. | k>-3且k≠1 | D. | k<5且k≠1 |
科目:初中数学 来源:2017届广西马山县民族中学春季学期第一次月考八年级数学试卷(解析版) 题型:单选题
等腰三角形腰长为13cm,底边长为10cm,则其面积为 ( )
A. 30 B. 40
B. 40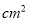 C. 50
C. 50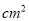 D. 60
D. 60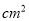
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知双曲线y=$\frac{k}{x}$,经过点D(6,1),点C是双曲线第三象限上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.
如图,已知双曲线y=$\frac{k}{x}$,经过点D(6,1),点C是双曲线第三象限上的动点,过C作CA⊥x轴,过D作DB⊥y轴,垂足分别为A,B,连接AB,BC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一慢车和一快车沿相同路线从A地到B地,所行的路程y(千米)与时间x(时)的函数图象如图所示,试根据图象,回答下列问题:
一慢车和一快车沿相同路线从A地到B地,所行的路程y(千米)与时间x(时)的函数图象如图所示,试根据图象,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com