
【题目】如图,以△ABC的三边为边在BC的同侧分别作三个等边三角形△ABD,△BCE,△ACF,请解答下列问题:
(1)求证:四边形AFED是平行四边形;
(2)当△ABC满足 时,四边形AFED是矩形.
当△ABC满足 时,四边形AFED是菱形.
当△ABC满足 时,四边形AFED是正方形.

【答案】(1)见解析; (2)![]() ; ∠BAC≠60°且AB=AC;
; ∠BAC≠60°且AB=AC;![]() 且AB=AC
且AB=AC
【解析】
(1)根据全等三角形的判定定理SAS证得△BDE≌△BAC,所以DE=AC=AF,同理可证△ABC≌△FEC,得出EF=AB=AD,所以四边形ADEF为平行四边形;
(2)根据ADEF是矩形,则可得出![]() ,利用在点A处组成的周角即可算出∠BAC的度数.
,利用在点A处组成的周角即可算出∠BAC的度数.
当AB=AC且∠BAC≠60°时,根据菱形的判定推出即可;
在四边形AEDF是矩形的条件下再加AB=AC,即可得出结论.
(1)证明:四边形ADEF是平行四边形.
理由:∵△ABD,△BEC都是等边三角形,
∴BD=AB,BE=BC,∠DBA=∠EBC=60°,
∴∠DBE=60°-∠EBA,∠ABC=60°-∠EBA,
∴∠DBE=∠ABC,
在△DBE和△ABC中
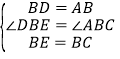
∴△DBE≌△ABC,
∴DE=AC,
又∵△ACF是等边三角形,
∴AC=AF,∴DE=AF.
同理可得:△ABC≌△FEC,即EF=AB=DA.
∵DE=AF,DA=EF,
∴四边形ADEF为平行四边形;
(2)解:当△ABC满足∠BAC=150°时,四边形ADEF是矩形;
理由:若四边形ADEF为矩形,则∠DAF=90°,
∵∠DAB=∠FAC=60°,
∴∠BAC=360°-∠DAB-∠FAC-∠DAF=360°-60°-60°-90°=150°,
∴当△ABC满足∠BAC=150°时,四边形ADEF是矩形;
∵当∠BAC=60°时,四边形ADEF中的A点与E点重合,此时以A、D、E、F为顶点的四边形不存在.
∴当∠BAC≠60°且AB=AC时,四边形AFED是菱形,
理由:∵由(1)知:四边形AFED是平行四边形;AD=AB=EF,AC=DE=AF,
∵AB=AC,∴AD=AF,
∴平行四边形AFED是菱形;
当∠BAC=150°且AB=AC,四边形ADEF是正方形.
理由:∵∠BAC=150°时,四边形ADEF是矩形;
∵AB=AC时,四边形AFED是菱形;
∴当∠ABC=150°,AB=AC时,四边形ADEF是正方形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,小华用黑白棋子组成的一组图案,第1个图案由1个黑子组成,第2个图案由1个黑子和6个白子组成,第3个图案由13个黑子和6个白子组成,按照这样的规律排列下去,则第8个图案中共有( )个棋子.

A.159B.169C.172D.132
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥CD,要使四边形ABCD为平行四边形,则应添加的条件是______.(添加一个条件即可,不添加其它的点和线).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场进行促销,购物满额即可获得1次抽奖机会,抽奖袋中装有红色、黄色、白色三种除颜色外都相同的小球,从袋子中摸出1个球,红色、黄色、白色分别代表一、二、三等奖.
(1)若小明获得1次抽奖机会,小明中奖是______事件;(填随机、必然、不可能)
(2)小明观察一段时间后发现,平均每6个人中会有1人抽中一等奖、2人抽中二等奖,若袋中共有18个球,请你估算袋中白球的数量;
(3)在(2)的条件下,如果在抽奖袋中增加3个黄球,那么抽中一等奖的概率会怎样变化?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明坐在堤边A处垂钓,河堤AC与水平面的夹角为30°,AC的长为 ![]() 米,钓竿AO与水平线的夹角为60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.
米,钓竿AO与水平线的夹角为60°,其长为3米,若AO与钓鱼线OB的夹角为60°,求浮漂B与河堤下端C之间的距离.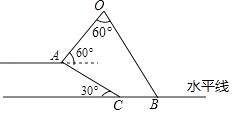
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上有一点E,且EF=ED.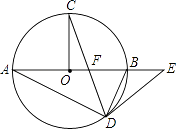
(1)求证:DE是⊙O的切线;
(2)若OF:OB=1:3,⊙O的半径R=3,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,∠C=90°,点D是AB的中点,点E,F分别在BC,AC上,且AF=CE.
(1)填空:∠A的度数是 .
(2)探究DE与DF的关系,并给出证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】星期天,小明从家里出发到图书馆去看书,再回到家.他离家的距离y(千米)与时间t(分钟)的关系如图所示.

根据图像回答下列问题:
(1)小明家离图书馆的距离是________千米;
(2)小明在图书馆看书的时间为________小时;
(3)小明去图书馆时的速度是________千米/小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点A、C、B不在同一条直线上,AD∥BE.
(1)如图①,当∠A=48°,∠B=128°时,求∠C的度数;
(2)如图②,AQ、BQ分别为∠DAC、∠EBC的平分线所在直线,试探究∠C与∠AQB的数量关系;
(3)如图③,在(2)的前提下,且有AC∥QB,QP⊥PB,直接写出∠DAC:∠ACB:∠CBE的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com