
【题目】观察下列式子:![]() ;
;![]() ;
;![]() ;…….
;…….
(1)请写出第4个等式:___________;
(2)请写出第n个等式____________;
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,将两张长为4,宽为1的矩形纸条交叉并旋转,使重叠部分成为一个菱形.旋转过程中,当两张纸条垂直时,菱形周长的最小值是4,那么菱形周长的最大值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,直线l:y=![]() 经过点A(4m,4),与y轴交于点B,抛物线
经过点A(4m,4),与y轴交于点B,抛物线![]() 经过点A,交y轴于点C.
经过点A,交y轴于点C.
⑴ 求直线l的解析式及抛物线的解析式;
⑵ 如图2,点D是直线l在第一象限内的一点,过点D作直线EF∥y轴,交抛物线于点E,交x轴于点F,连接AF,若∠CEF=∠CBA,求AF的长;
⑶ 在(2)的结论下,若点P是直线EF上一点,点Q是直线l上一点.当△PFA与△QPA全等时,直接写出点P和相应的点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知抛物线y=﹣x2﹣2x+3与x轴交于点A和点B,与y轴交于点C.
(1)直接写出A,B,C三点的坐标:A ;B ;C ;
(2)在该抛物线的对称轴上是否存在点P,时△APC的周长最小,若存在,求出点P的坐标,若不存在,请说明理由.
(3)如图②,若点E为第二象限抛物线上的一动点,连接BE、CE,求四边形BOCE面积的最大值,并求此时E点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 在
在![]() 内并排
内并排![]() 不重叠
不重叠![]() 放入边长为1的小正方形纸片,第一层小纸片的一条边都在AB上,首尾两个正方形各有一个顶点分别在AC、BC上,依次这样摆放上去,则最多能摆放
放入边长为1的小正方形纸片,第一层小纸片的一条边都在AB上,首尾两个正方形各有一个顶点分别在AC、BC上,依次这样摆放上去,则最多能摆放![]()
![]() 个小正方形纸片.
个小正方形纸片.
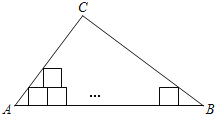
A. 14个 B. 15个 C. 16个 D. 17个
查看答案和解析>>
科目:初中数学 来源: 题型:
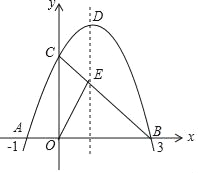
【题目】如图,已知抛物线y=﹣x2+bx+c与x轴交于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC交抛物线的对称轴于点E、D是抛物线的顶点.
(1)求此抛物线的解析式;
(2)求点C和点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据新华社北京2019年4月10日报道:神秘天体黑洞终于被人类 “看到”了。
上世纪初,爱因斯坦预言了黑洞的存在,这是一种体积极小而质量极大的天体,引力非常强 ,以至于周围一定区域内包括光在内的任何物体都无法逃逸而被黑洞吸引吞噬。每个星球都有一个逃逸速度,若周围物体速度低于该逃逸速度,物体将被星球吸引,只有物体速度达到逃逸速度,才可能完全逃脱星球的引力束缚而飞出该星球。逃逸速度的计算公式为![]() (式中的G是万有引力常量
(式中的G是万有引力常量![]() )。
)。
(1)如果星球A的质量![]() ,星球半径
,星球半径![]() ,那该星球的逃逸速度V为多大呢?同学们运用上面的公式计算一下就知道了。(单位已经换算好,不需要考虑单位换算了,结果V的单位为:m/s)
,那该星球的逃逸速度V为多大呢?同学们运用上面的公式计算一下就知道了。(单位已经换算好,不需要考虑单位换算了,结果V的单位为:m/s)
(2)从逃逸速度的计算公式可以看出,当星球的质量不变而半径变小时,逃逸速度V将会增大,这也意味着该星球在质量不变体积变小时将吸引更多的周围物体使其无法逃逸。光速是目前所发现的自然界物体运动的最大速度,没有比光子速度更快的物体,可以想象,当星球A的半径R如果缩小到某个很小数值![]() 时,其逃逸速度就会超过光速
时,其逃逸速度就会超过光速![]() ,则星球A上的所有物体(包括光子)都无法逃脱该星球的引力,于是星球A塌缩成了一个黑洞。我们来计算一下,此时“黑洞”星球A的半径
,则星球A上的所有物体(包括光子)都无法逃脱该星球的引力,于是星球A塌缩成了一个黑洞。我们来计算一下,此时“黑洞”星球A的半径![]() 为多大呢?
为多大呢?
(提示:将逃逸速度公式变形为![]() ,将V用光速c代替得到
,将V用光速c代替得到![]() ,单位已经换算好,不需要考虑单位换算了,结果
,单位已经换算好,不需要考虑单位换算了,结果![]() 的单位为:m)
的单位为:m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种商品按销售量分三部分制定销售单价,如表:
销售量 | 单价 |
不超过100件的部分 | 2.5元/件 |
超过100件不超过300件的部分 | 2.2元/件 |
超过300件的部分 | 2元/件 |
(1)若买100件花 元,买300件花 元;
(2)小明买这种商品花了360元,列方程求购买这种商品多少件?
(3)若小明花了![]() 元(
元(![]() ),恰好购买
),恰好购买![]() 件这种商品,求
件这种商品,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6.点P从点A出发,沿AC以每秒1个单位的速度向终点C运动;点Q从点C出发,沿C-B-A以每秒2个单位的速度向终点A运动.当点P停止运动时,点Q也随之停止.点P、Q同时出发,设点P的运动时间为t(秒).
(1)求AB的长.
(2)用含t的代数式表示CP的长.
(3)设点Q到CA的距离为y,求y与t之间的函数关系式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com