
分析 先把已知等式转化为绝对值与完全平方式的和的形式,然后由非负数的性质得到a、b、c的值,将其代入所求的代数式进行求值即可.
解答 解:因为$|{a-2}|+{b^2}+4b+4+\sqrt{{c^2}-c+\frac{1}{4}}=0$,
可得:a=2,b=-2,c=$\frac{1}{2}$,
所以把a=2,b=-2,c=$\frac{1}{2}$代入$\sqrt{b^2}•\sqrt{a}•\sqrt{c}$=2×$\sqrt{2}×\frac{\sqrt{2}}{2}$=2.
点评 本题考查了二次根式的化简,非负数的性质.
初中阶段有三种类型的非负数:(1)绝对值;(2)偶次方;(3)二次根式(算术平方根).当它们相加和为0时,必须满足其中的每一项都等于0.根据这个结论可以求解这类题目.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 已知点A,B分别在x轴的负半轴和正半轴上,OA,OB的长分别是一元二次方程x2-5x+6=0的两个根,且OA>OB,点C的坐标为(0,-4),点D在y轴上,直线AD平分∠CAB.
已知点A,B分别在x轴的负半轴和正半轴上,OA,OB的长分别是一元二次方程x2-5x+6=0的两个根,且OA>OB,点C的坐标为(0,-4),点D在y轴上,直线AD平分∠CAB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,矩形ABCD的顶点A与坐标原点O重合,B(4,0),D(0,3),点E从点A出发,沿射线AB移动,以CE为直径作⊙M,点F为⊙M与射线DB的公共点,连接EF、CF,过点E作EG⊥EF,EG与⊙M相交于点G,连接CG.
如图,在平面直角坐标系中,矩形ABCD的顶点A与坐标原点O重合,B(4,0),D(0,3),点E从点A出发,沿射线AB移动,以CE为直径作⊙M,点F为⊙M与射线DB的公共点,连接EF、CF,过点E作EG⊥EF,EG与⊙M相交于点G,连接CG.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
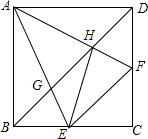 如图,正方形ABCD中,点E,F分别在BC、DC上,∠EAF=45°,AE,AF分别交BD于G,H,下列结论
如图,正方形ABCD中,点E,F分别在BC、DC上,∠EAF=45°,AE,AF分别交BD于G,H,下列结论| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A | B | |
| 进价(元/台) | 500 | 600 |
| 售价(元/台) | 600 | 790 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com