
已知:△ABD和△CBD关于直线BD对称(点A的对称点是点C),点E、F分别是线段BC和线段BD上的点,且点F在线段EC的垂直平分线上,连接AF、AE,AE交BD于点G.
(1)如图l,求证:∠EAF=∠ABD;
(2)如图2,当AB=AD时,M是线段AG上一点,连接BM、ED、MF,MF的延长线交ED于点N,∠MBF= ∠BAF,AF=
∠BAF,AF= AD,请你判断线段FM和FN之间的数量关系,并证明你的判断是正确的.
AD,请你判断线段FM和FN之间的数量关系,并证明你的判断是正确的.
(1)证明见解析;(2)FM=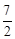 FN ,证明见解析.
FN ,证明见解析.
解析试题分析:(1)连接FE、FC,先证△ABF、△CBF全等,得∠FEC=∠BAF,通过四边形ABEF与三角形AEF内角和导出.
(2)先由△AFG∽△BFA,推出∠AGF=∠BAF,再得BG=MG,通过△AGF∽△DGA,导出GD=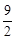 a. FD=
a. FD=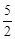 a,过点F作FQ∥ED交AE于Q,通过BE∥AD得线段成比例,设EG=2k,BG=MG=3k,GQ=
a,过点F作FQ∥ED交AE于Q,通过BE∥AD得线段成比例,设EG=2k,BG=MG=3k,GQ=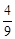 EG=
EG=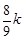 ,MQ=3k+
,MQ=3k+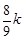 =
=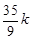 ,
,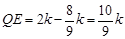 ,从而FM=
,从而FM=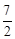 FN.
FN.
(1)如图,连接FE、FC,
∵点F在线段EC的垂直平分线上,∴FE="FC." ∴∠l=∠2.
∵△ABD和△CBD关于直线BD对称,∴AB=CB,∠4=∠3, BF=BF.
∴△ABF≌△CBF(SAS). ∴∠BAF=∠2,FA=FC.
∴FE=FA,∠1=∠BAF. ∴∠5=∠6 .
∵∠l+∠BEF=1800,∴∠BAF+∠BEF=1800.
∵∠BAF+∠BEF+∠AFE+∠ABE=3600,∴∠AFE+∠ABE=1800.
又∵∠AFE+∠5+∠6=1800,∴∠5+∠6=∠3+∠4.
∴∠5=∠4,即∠EAF=∠ABD.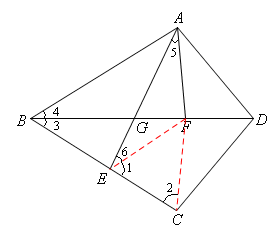
(2)FM=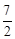 FN ,证明如下:
FN ,证明如下:
如图,由(1)可知∠EAF=∠ABD,
又∵∠AFB=∠GFA,∴△AFG∽△BFA. ∴∠AGF=∠BAF。
又∵∠MBF=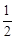 ∠BAF.∠MBF=
∠BAF.∠MBF=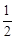 ∠AGF,∠AGF=∠MBG+∠BMG,∴∠MBG=∠BMG.∴BG=MG.
∠AGF,∠AGF=∠MBG+∠BMG,∴∠MBG=∠BMG.∴BG=MG.
∵AB=AD,∴∠ADB=∠ABD=∠EAF.
∵∠FGA=∠AGD,∴△AGF∽△DGA. ∴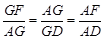 .
.
∵AF=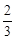 AD,∴
AD,∴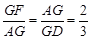 .
.
设GF="2a" ,AG=3a,则GD=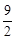 a. ∴FD=
a. ∴FD=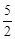 a.
a.
∵∠CBD=∠ABD, ∠ABD=∠ADB,∴∠CBD=∠ADB. ∴BE∥AD.
∴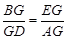 . ∴
. ∴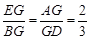 .
.
设EG=2k,∴BG=MG=3k.
过点F作FQ∥ED交AE于Q,
∴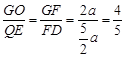 .∴
.∴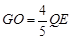 .
.
∴GQ=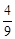 EG=
EG=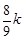 ,MQ=3k+
,MQ=3k+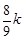 =
=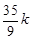 . ∴
. ∴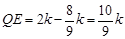 .
.
∵FQ∥ED,∴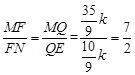 . ∴FM=
. ∴FM=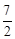 FN.
FN.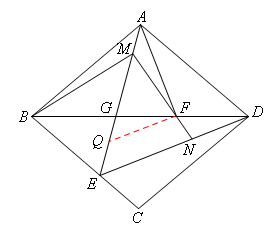
考点:1.轴对称问题;2.线段垂直平分线的性质;3.全等三角形的判定和性质;4.等腰三角形的性质;5.三角形内角和定理;6.相似三角形的判定和性质;7.平行的判定和性质;8.待定系数法的应用.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:解答题
如图,矩形ABCD的顶点坐标分别为A(1,1),B(2,1),C(2,3),D(1,3).
(1)将矩形各顶点的横、纵坐标都乘以2,写出各对应点A1B1C1D1的坐标;顺次连接A1B1C1D1,画出相应的图形.
(2)求矩形A1B1C1D1与矩形ABCD的面积的比 _________ .
(3)将矩形ABCD的各顶点的横、纵坐标都扩大n倍(n为正整数),得到矩形AnBnCnDn,则矩形AnBnCnDn与矩形ABCD的面积的比为 _________ .
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
问题情境:如图1,直角三角板ABC中,∠C=90°,AC=BC,将一个用足够长的的细铁丝制作的直角的顶点D放在直角三角板ABC的斜边AB上,再将该直角绕点D旋转,并使其两边分别与三角板的AC边、BC边交于P、Q两点。
问题探究:(1)在旋转过程中,
①如图2,当AD=BD时,线段DP、DQ有何数量关系?并说明理由。
②如图3,当AD=2BD时,线段DP、DQ有何数量关系?并说明理由。
③根据你对①、②的探究结果,试写出当AD=nBD时,DP、DQ满足的数量关系为_______________(直接写出结论,不必证明)
(2)当AD=BD时,若AB=20,连接PQ,设△DPQ的面积为S,在旋转过程中,S是否存在最小值或最大值?若存在,求出最小值或最大值;若不存在,请说明理由。
图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图, Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E为BC边的中点,连接DE.
(1)求证:DE与⊙O 相切.
(2)若tanC= ,DE=2,求AD的长.
,DE=2,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,Rt△ABC中,∠ACB=90°,AC=6 cm,BC=8 cm,动点P从点B出发,在BA边上以每秒5 cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4 cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
(1)若△BPQ与△ABC相似,求t的值;
(2)连接AQ、CP,若AQ⊥CP,求t的值;
(3)试证明:PQ的中点在△ABC的一条中位线上.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,在等腰Rt△ABC中,∠C=90°,正方形DEFG的顶点D在边AC上,点E,F在边AB上,点G在边BC上.
⑴求证:△ADE≌△BGF;
⑵若正方形DEFG的面积为16,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知,如图,在平行四边形ABCD中,E、F分别是边BC、CD上的点,且EF∥BD,AE、AF分别交BD于点G和点H,BD=12,EF=8。求:(1) 的值。(2)线段GH的长。
的值。(2)线段GH的长。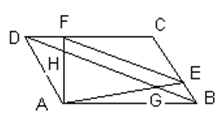
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
小明对直角三角形很感兴趣. △ABC中,∠ACB=90°,D是AB上任意一点,连接DC,作DE⊥DC,EA⊥AC,DE与AE交于点E.请你跟着他一起解决下列问题: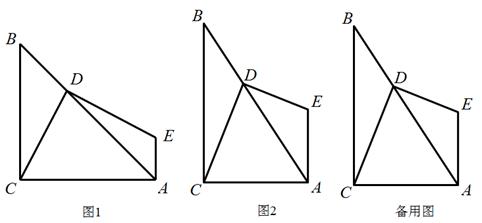
(1)如图1,若△ABC是等腰直角三角形,则DE,DC有什么数量关系?请给出证明.
(2)如果换一个直角三角形,如图2,∠CBA=30°,则DE,DC又有什么数量关系?请给出证明.
(3)由(1)、(2)这两种特殊情况,小明提出问题:如果直角三角形ABC中,BC=mAC,那DE, DC有什么数量关系?请给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com