
如图,已知梯形ABCD中,AB∥CD,∠ABC=![]() ,AB=8,CD=6,BC=
,AB=8,CD=6,BC=![]() .在AB边上取动点P,连结DP,作PQ⊥DP,使PQ交射线BC于点E.设AP=x,BE=y.
.在AB边上取动点P,连结DP,作PQ⊥DP,使PQ交射线BC于点E.设AP=x,BE=y.

(1)试写出y关于自变量x的函数关系式(不要求写出自变量x的取值范围);
(2)如果在线段AB上能找到不同的两点P1、P2,使按上述作法作得的点E都与点C重合,试求m的取值范围,并用m表示相应的AP1、AP2的长.
|
解:(1)过点D作DF⊥AB,垂足为F,易证△BPE∽△FDP. ∴ ∴y=- 此即y关于自变量x的函数关系式. (2)当E点与C点重合时,即y= 据题意,m的取值应使这个关于x的方程有两个相异实根,且使点P1、P2都在线段AB上,于是有Δ=(-10)2-4(16+m)=36-4m>0,解之得m<9.又据题意知m>0,所以m的取值范围为0<m<9.而 x= 当0<m<9时,0<9-m<9,∴0< |
|
本题与上题在题型以及所考查的知识点方面有很多相近之处.需要注意的是,本题求得的函数关系式中,除含有自变量x外,还有一个以字母表示的量,这就是m.由于m也是可以变化的,所以所得的表达式也可以看成是x、m、y三个变量所满足的一个关系式.在第(2)小题中,要求点E与点C重合,这就相当于在上述关系式中令y= |


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
| S1 | S2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
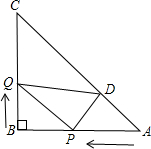 点到达终点时,另一点也随之停止.过Q作QD∥AB交AC于点D,连接PD,设运动时间为t秒时,四边形BQDP的面积为s.
点到达终点时,另一点也随之停止.过Q作QD∥AB交AC于点D,连接PD,设运动时间为t秒时,四边形BQDP的面积为s.查看答案和解析>>
科目:初中数学 来源: 题型:阅读理解

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com