
【题目】反比例函数![]() (
(![]() 为常数.且
为常数.且![]() )的图象经过点
)的图象经过点![]() .
.![]() .
.
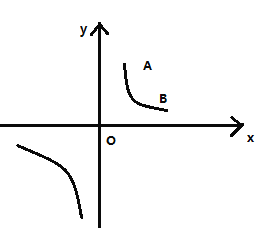
(1)求反比例函数的解析式及![]() 点的坐标;
点的坐标;
(2)在![]() 轴上找一点
轴上找一点![]() .使
.使![]() 的值最小,
的值最小,
①求满足条件的点![]() 的坐标;②求
的坐标;②求![]() 的面积.
的面积.
【答案】(1)![]() ,B点坐标为(3,1);(2)①P点坐标为(
,B点坐标为(3,1);(2)①P点坐标为(![]() ,0);②
,0);②![]()
【解析】
(1)先把A点坐标代入![]() 求出k得到反比例函数解析式;然后把B(3,m)代入反比例函数解析式求出m得到B点坐标;
求出k得到反比例函数解析式;然后把B(3,m)代入反比例函数解析式求出m得到B点坐标;
(2)①作A点关于x轴的对称点A′,连接BA′交x轴于P点,则A′(1,-3),利用两点之间线段最短可判断此时PA+PB的值最小,再利用待定系数法求出直线BA′的解析式,然后求出直线与x轴的交点坐标即可得到P点坐标;
②根据![]() 的面积=梯形ABDC的面积-△PAC的面积-△PBD的面积计算即可.
的面积=梯形ABDC的面积-△PAC的面积-△PBD的面积计算即可.
解:(1)把A(1,3)代入![]() 得k=1×3=3,
得k=1×3=3,
∴反比例函数解析式为![]() ;
;
把B(3,m)代入![]() 得3m=3,解得m=1,
得3m=3,解得m=1,
∴B点坐标为(3,1);
(2)①作A点关于x轴的对称点A′,连接BA′交x轴于P点,则A′(1,-3),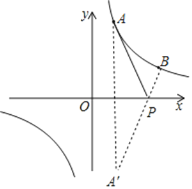
∵PA+PB=PA′+PB=BA′,
∴此时PA+PB的值最小,
设直线BA′的解析式为y=mx+n,
把A′(1,-3),B(3,1)代入得![]() ,解得
,解得![]() ,
,
∴直线BA′的解析式为y=2x-5,
当y=0时,2x-5=0,解得x=![]() ,
,
∴P点坐标为(![]() ,0);
,0);
②如图,连接AB,作BD⊥x轴于点D,设A A′与x轴交于点C,
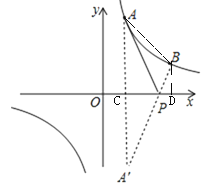
∵A(1,3),B(3,1),P(![]() ,0),
,0),
∴AC=3,BD=1,CD=2,CP=![]() ,PD=
,PD=![]() ,
,
∴![]() 的面积=梯形ABDC的面积-△PAC的面积-△PBD的面积
的面积=梯形ABDC的面积-△PAC的面积-△PBD的面积
=![]()
=![]()
=![]() .
.


 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:
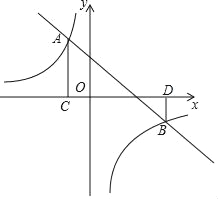
【题目】如图,直线y=﹣x+2与反比例函数y=![]() (k≠0)的图象交于A(a,3),B(3,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.
(k≠0)的图象交于A(a,3),B(3,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D.
(1)求a,b的值及反比例函数的解析式;
(2)若点P在直线y=﹣x+2上,且S△ACP=S△BDP,请求出此时点P的坐标;
(3)在x轴正半轴上是否存在点M,使得△MAB为等腰三角形?若存在,请直接写出M点的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲、乙两台包装机包装的质量为300g的袋装食品中各抽取10袋,测得其实际质量如下(单位:g)
甲:301,300,305,302,303,302,300,300,298,299
乙:305,302,300,300,300,300,298,299,301,305
(1)分别计算甲、乙这两个样本的平均数和方差;
(2)比较这两台包装机包装质量的稳定性.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:如图1设P是等边△ABC内一点,PA=6,PB=8,PC=10,求∠APB的度数.小君研究这个问题的思路是:将△ACP绕点A逆时针旋转60°得到△ABP',易证:△APP'是等边三角形,△PBP'是直角三角形,所以∠APB=∠APP'+∠BPP'=150°.

简单应用:(1)如图2,在等腰直角△ABC中,∠ACB=90°.P为△ABC内一点,且PA=5,PB=3,PC=2![]() ,则∠BPC= °.
,则∠BPC= °.
(2)如图3,在等边△ABC中,P为△ABC内一点,且PA=5,PB=12,∠APB=150°,则PC= .
拓展廷伸:(3)如图4,∠ABC=∠ADC=90°,AB=BC.求证:![]() BD=AD+DC.
BD=AD+DC.
(4)若图4中的等腰直角△ABC与Rt△ADC在同侧如图5,若AD=2,DC=4,请直接写出BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮用三枚质地均匀的硬币做游戏,游戏规则是:同时抛掷这三枚硬币,出现两枚正面向上,一枚正面向下,则小明赢;出现两枚正面向下,一枚正面向上,则小亮赢.这个游戏规则对双方公平吗?请你用树状图或列表法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方方驾驶小汽车匀速地从![]() 地行驶到
地行驶到![]() 地,行驶里程为
地,行驶里程为![]() 千米,设小汽车的行驶时间为
千米,设小汽车的行驶时间为![]() (单位:小时),行驶速度为
(单位:小时),行驶速度为![]() (单位:千米/小时),且全程速度限定为不超过
(单位:千米/小时),且全程速度限定为不超过![]() 千米/小时.
千米/小时.
(1)求![]() 关于
关于![]() 的函数表达式,并写出自变量
的函数表达式,并写出自变量![]() 的取值范围;
的取值范围;
(2)方方上午![]() 点驾驶小汽车从
点驾驶小汽车从![]() 地出发;
地出发;
①方方需在当天![]() 点
点![]() 分至
分至![]() 点(含
点(含![]() 点
点![]() 分和
分和![]() 点)间到达
点)间到达![]() 地,求小汽车行驶速度
地,求小汽车行驶速度![]() 的范围;
的范围;
②方方能否在当天![]() 点
点![]() 分前到达
分前到达![]() 地?说明理由.
地?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
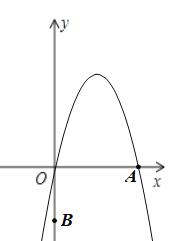
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,点
两点,点![]() .
.
(1)当![]() 时,求抛物线的顶点坐标及线段
时,求抛物线的顶点坐标及线段![]() 的长度;
的长度;
(2)若点![]() 关于点
关于点![]() 的对称点
的对称点![]() 恰好也落在抛物线上,求
恰好也落在抛物线上,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为半圆
为半圆![]() 的直径,
的直径,![]() 交
交![]() 于
于![]() ,
,![]() 为
为![]() 延长线上一动点,
延长线上一动点,![]() 为
为![]() 中点,
中点,![]() ,交半径
,交半径![]() 于
于![]() ,连
,连![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 为定值.其中正确结论的个数为( )
为定值.其中正确结论的个数为( )
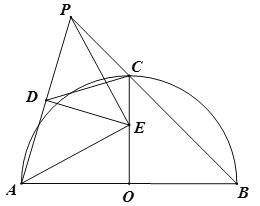
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com