
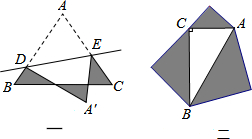
分析 如图一,由折叠可得阴影部分图形的周长正好等于原等边三角形的周长;
如图二,根据勾股定理和等腰直角三角形的面积公式,可以证明:以直角三角形的两条直角边为斜边的等腰直角三角形的面积和等于以斜边为斜边的等腰直角三角形的面积.则阴影部分的面积即为以斜边为斜边的等腰直角三角形的面积的2倍.
解答 解:如图一中,由折叠可得AD=A′D;AE=A′E,
∴阴影部分图形的周长为AB+BC+AC=3cm.
故答案为3.
如图二中,在Rt△AHC中,AC2=AH2+HC2,AH=HC,
∴AC2=2AH2,
∴HC=AH=$\frac{AC}{\sqrt{2}}$,
同理CF=BF=$\frac{CB}{\sqrt{2}}$,BE=AE=$\frac{AB}{\sqrt{2}}$,
在Rt△ABC中,AB2=AC2+BC2,AB=4,
S阴影=S△AHC+S△BFC+S△AEB=$\frac{1}{2}$HC•AH+$\frac{1}{2}$CF•BF+$\frac{1}{2}$AE•BE,
=$\frac{1}{2}$×($\frac{AC}{\sqrt{2}}$)2+$\frac{1}{2}$×($\frac{BC}{\sqrt{2}}$)2+$\frac{1}{2}$×($\frac{AB}{\sqrt{2}}$)2
=$\frac{1}{4}$(AC2+BC2+AB2)
=$\frac{1}{4}$(AB2+AB2)
=$\frac{1}{4}$×2AB2
=$\frac{1}{2}$×AB2
=$\frac{1}{2}$×42
=8.
故答案为 8.
点评 本题考查折叠的问题、勾股定理、三角形的周长以及面积等知识,难度适中,解题关键是运用勾股定理证明三个等腰直角三角形的面积之间的关系,属于中考常考题型.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
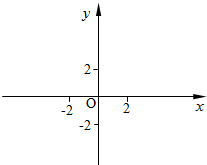 已知一条直线y=kx+b在y轴上的截距为2,它与x轴、y轴的交点分别为A、B,且△ABO的面积为4.
已知一条直线y=kx+b在y轴上的截距为2,它与x轴、y轴的交点分别为A、B,且△ABO的面积为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对旅客上飞机前的安检 | |
| B. | 了解全班同学每周体育锻炼的时间 | |
| C. | 调查奥运会金牌获得者的兴奋剂使用情况 | |
| D. | 调查我国居民对汽车废气污染环境的看法 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x-2=x | B. | x2-2x=2x | C. | x-2=2x | D. | x=2x-4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com