
【题目】已知直线 y= -x+5交x轴于A,交y轴于B,直线y=2x﹣4与x轴于D,与直线AB相交于点C.
(1)求点C的坐标;
(2)求四边形BODC的面积.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某工程队承包了某标段全长1800米的过江隧道施工任务,甲、乙两个班组分别从东、西两端同时掘进.已知甲组比乙组平均每天多掘进2米,经过5天施工,两组共掘进了60米.
(1)求甲、乙两班组平均每天各掘进多少米?
(2)为加快工程进度,通过改进施工技术,在剩余的工程中,甲组平均每天能比原来多掘进2米,乙组平均每天能比原来多掘进1米.按此施工进度,能够比原来少用多少天完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某测量队在山脚A处测得山上树顶仰角为45°(如图),测量队在山坡上前进600米到D处,再测得树顶的仰角为60°,已知这段山坡的坡角为30°,如果树高为15米,则山高为( )(精确到1米, ![]() =1.732).
=1.732).
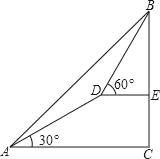
A. 585米 B. 1014米 C. 805米 D. 820米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
数学问题:已知![]() ,且
,且![]() ,
,![]() ,试确定
,试确定![]() 的取值范围.
的取值范围.
问题解法:![]() ,
,![]() .
.
又![]() ,
,![]() ,
,![]() .
.
又![]() ,
,![]() .①
.①
同理得![]() .②
.②
由②![]() ①得
①得![]() ,
,
![]() 的取值范围是
的取值范围是![]() .
.
完成任务:
(1)在数学问题中的条件下,写出![]() 的取值范围是_____.
的取值范围是_____.
(2)已知![]() ,且
,且![]() ,
,![]() ,试确定
,试确定![]() 的取值范围;
的取值范围;
(3)已知![]() ,
,![]() ,若
,若![]() 成立,试确定
成立,试确定![]() 的取值范围(结果用含a的式子表示).
的取值范围(结果用含a的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读,并探究相关的问题:
(阅读)
![]() 的几何意义是数轴上
的几何意义是数轴上![]() ,
,![]() 两数所对的点
两数所对的点![]() ,
,![]() 之间的距离,记作
之间的距离,记作![]() ,如
,如![]() 的几何意义:表示
的几何意义:表示![]() 与
与![]() 两数在数轴上所对应的两点之间的距离;
两数在数轴上所对应的两点之间的距离;![]() 可以看做
可以看做![]() ,几何意义可理解为
,几何意义可理解为![]() 与
与![]() 两数在数轴上对应的两点之间的距离.
两数在数轴上对应的两点之间的距离.
(1)数轴上表示![]() 和
和![]() 的两点
的两点![]() 和
和![]() 之间的距离可表示为____________;如果
之间的距离可表示为____________;如果![]() ,求出
,求出![]() 的值;
的值;
(2)探究:![]() 是否存在最小值,若存在,求出最小值;若不存在,请说明理由;
是否存在最小值,若存在,求出最小值;若不存在,请说明理由;
(3)求![]() 的最小值,并指出取最小值时
的最小值,并指出取最小值时![]() 的值.
的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
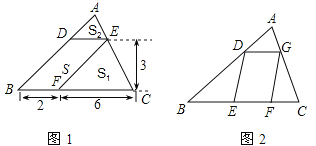
【题目】问题背景:(1)如图1,△ABC中,DE∥BC分别交AB,AC于D,E两点,过点E作EF∥AB交BC于点F。请按图示数据填空:四边形DBFE的面积![]() ______,△EFC的面积
______,△EFC的面积![]() ______,△ADE的面积
______,△ADE的面积![]() ______。
______。
探究发现:(2)在(1)中,若![]() ,
, ![]() ,DE与BC间的距离为
,DE与BC间的距离为![]() 。请证明
。请证明![]() 。
。
拓展迁移:(3)如图2,□DEFG的四个顶点在△ABC的三边上,若△ADG、△DBE、△GFC的面积分别为2、5、3,试利用(2)中的结论求△ABC的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E、F在AC上,AD=BC,AD//BC,则添加下列哪个条件后,仍无法判定△ADF≌△CBE的是
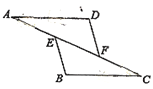
A. DF=BE B. ∠D=∠B C. AE=CF D. DF//BE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在已知的△ABC中,按以下步骤作图:①分别以B,C为圆心,以大于![]() BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )
BC的长为半径作弧,两弧相交于两点M,N;②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )

A. 90°B. 95°C. 100°D. 105°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一.数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=132米,求观景亭D到南滨河路AC的距离约为多少米?(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com