
| A. | 5 | B. | 1±$\sqrt{3}$ | C. | 5或1-$\sqrt{3}$ | D. | 5或1±$\sqrt{3}$ |
分析 因为a2=2-2a,b2=2-2b可以变化为$\left\{\begin{array}{l}{{a}^{2}+2a+1=3}\\{{b}^{2}+2b+1=3}\end{array}\right.$即$\left\{\begin{array}{l}{(a+1)^{2}=3}\\{(a+1)^{2}=3}\end{array}\right.$,从而可以求出a,b,然后把它们的值代入得原式即可求出结果.
解答 解:∵a2=2-2a,b2=2-2b,
∴可以变化为为$\left\{\begin{array}{l}{{a}^{2}+2a+1=3}\\{{b}^{2}+2b+1=3}\end{array}\right.$即$\left\{\begin{array}{l}{(a+1)^{2}=3}\\{(a+1)^{2}=3}\end{array}\right.$,
解得a=±$\sqrt{3}$-1,b=$±\sqrt{3}$,
把$\left\{\begin{array}{l}{a=\sqrt{3}-1}\\{b=\sqrt{3}-1}\end{array}\right.$代入得原式=$\sqrt{3}$+1;
把$\left\{\begin{array}{l}{a=-\sqrt{3}-1}\\{b=\sqrt{3}-1}\end{array}\right.$代入得原式=-5;
把$\left\{\begin{array}{l}{a=\sqrt{3}-1}\\{b=-\sqrt{3}-1}\end{array}\right.$代入得原式=-5;
把$\left\{\begin{array}{l}{a=-\sqrt{3}-1}\\{b=-\sqrt{3}-1}\end{array}\right.$代入得原式=1-$\sqrt{3}$.
所以此题的答案为$\sqrt{3}$+1,1-$\sqrt{3}$,-5.
故选D.
点评 本题考查了一元二次方程根与系数的关系,解题的关键是利用完全平方公式先求得a,b的值,再分情况分别代入求值计算.


科目:初中数学 来源: 题型:解答题
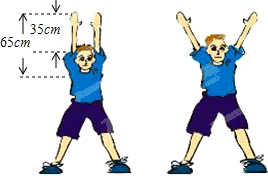 一位同学的手臂长65cm,当他竖直举高双臂时,指尖高出头顶35cm.当他的手臂与水平方向成60°时,他的指尖高出头顶多少厘米(精确到0.1cm)
一位同学的手臂长65cm,当他竖直举高双臂时,指尖高出头顶35cm.当他的手臂与水平方向成60°时,他的指尖高出头顶多少厘米(精确到0.1cm)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
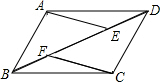 如图,在?ABCD中,点E、F在BD上,且BF=DE,
如图,在?ABCD中,点E、F在BD上,且BF=DE,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
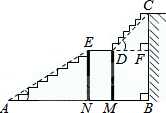 某宾馆大厅到二楼的楼梯设计图如下,已知BC=6米,AB=9米,中间平台宽度DE为2米.DM、DN为平台的两根支柱,DM、EN垂直于AB,垂足分别为M、N,∠EAB=30°,∠CDF=45°.求DM和BC的水平距离BM.
某宾馆大厅到二楼的楼梯设计图如下,已知BC=6米,AB=9米,中间平台宽度DE为2米.DM、DN为平台的两根支柱,DM、EN垂直于AB,垂足分别为M、N,∠EAB=30°,∠CDF=45°.求DM和BC的水平距离BM.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
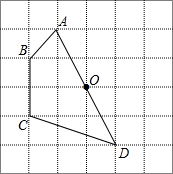 如图,正方形网格中的每一个小正方形的边长都是1,四边形ABCD的四个顶点都在格点上,O为AD边的中点,若把四边形ABCD绕着点O顺时针旋转,试解决下列问题:
如图,正方形网格中的每一个小正方形的边长都是1,四边形ABCD的四个顶点都在格点上,O为AD边的中点,若把四边形ABCD绕着点O顺时针旋转,试解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com