
分析 根据分式的运算法则即可求出答案.
解答 解:(1)原式=$\frac{4}{a-2}$+$\frac{(a-2)(a+2)}{a-2}$
=$\frac{{4+{a^2}-4}}{a-2}$
=$\frac{a^2}{a-2}$
(2)原式=$[{\frac{{{{(x-2)}^2}}}{(x+2)(x-2)}-\frac{{{{(x+2)}^2}}}{(x+2)(x-2)}}]•\frac{x(x-2)}{x^2}$
=$\frac{-8x}{(x+2)(x-2)}•\frac{(x-2)}{x}$
=$\frac{-8}{x+2}$
点评 本题考查分式的运算,解题的关键是熟练运用分式的运算法则,本题属于基础题型.


科目:初中数学 来源: 题型:选择题
| A. | 甲比较稳定 | B. | 乙比较稳定 | C. | 甲、乙一样稳定 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
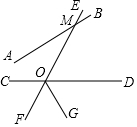 如图,已知直线EF与AB交于点M,与CD交于点O,OG平分∠DOF,若∠COM=120°,∠EMB=$\frac{1}{2}$∠COF.
如图,已知直线EF与AB交于点M,与CD交于点O,OG平分∠DOF,若∠COM=120°,∠EMB=$\frac{1}{2}$∠COF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
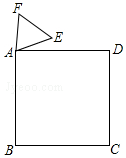 如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕其顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小是15°或165°.
如图,正方形ABCD与正三角形AEF的顶点A重合,将△AEF绕其顶点A旋转,在旋转过程中,当BE=DF时,∠BAE的大小是15°或165°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若一个数的绝对值是它的相反数,则这个数为负数 | |
| B. | 任何数的绝对值都是正数 | |
| C. | 两个数的绝对值相等,则这两个数相等 | |
| D. | 一个正数的绝对值一定是正数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com