
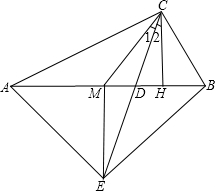
 已知:如图,在Rt△ABC中,∠ACB=90°,点M是AB边的中点,CH⊥AB于点H,CD平分∠ACB.
已知:如图,在Rt△ABC中,∠ACB=90°,点M是AB边的中点,CH⊥AB于点H,CD平分∠ACB.分析 (1)根据直角三角形斜边上的中线等于斜边的一半得到AM=CM=BM,由等腰三角形到性质得到∠CAB=∠ACM,由余角的性质得到∠CAB=∠BCH,等量代换得到∠BCH=∠ACM,根据角平分线的性质得到∠ACD=∠BCD,即可得到结论;
(2)根据EM⊥AB,CH⊥AB,得到EM∥AB,由平行线的性质得到∠HCD=∠MED,由于∠HCD=∠MCD,于是得到∠MCD=∠MED,即可得到结论;
(3)根据 CM=EM AM=CM=BM,于是得到EM=AM=BM,推出△AEB是直角三角形,由于 EM垂直平分AB,得到EA=EB于是得到结论.
解答 证明:(1)Rt△ABC中,∠ACB=90°,
∵M是AB边的中点,
∴AM=CM=BM,
∴∠CAB=∠ACM,
∴∠CAB=90-∠ABC,
∵CH⊥AB,
∴∠BCH=90-∠ABC,
∴∠CAB=∠BCH,
∴∠BCH=∠ACM,
∵CD平分∠ACB,
∴∠ACD=∠BCD,
∴∠ACD-∠ACM=∠BCD-∠BCH,
即∠1=∠2;
(2)∵EM⊥AB,CH⊥AB,
∴EM∥CH,
∴∠HCD=∠MED,
∵∠HCD=∠MCD,
∴∠MCD=∠MED,
∴CM=EM;
(3)△AEB是等腰直角三角形,
∵CM=EM AM=CM=BM,
∴EM=AM=BM,
∴△AEB是直角三角形,
∵EM垂直平分AB,
∴EA=EB,
∴△AEB是等腰三角形,
∴△AEB是等腰直角三角形.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半,等腰直角三角形的判定和性质,角平分线的定义,线段垂直平分线的性质,等腰三角形的性质,熟练掌握各定理是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
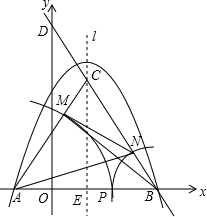 如图所示,抛物线y=-x2+2x+8与x轴交于A、B两点,直线BD的解析式为y=-2$\sqrt{3}x$+8$\sqrt{3}$,抛物线的对称轴l与直线BD交于点C、与x轴交于点E.
如图所示,抛物线y=-x2+2x+8与x轴交于A、B两点,直线BD的解析式为y=-2$\sqrt{3}x$+8$\sqrt{3}$,抛物线的对称轴l与直线BD交于点C、与x轴交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
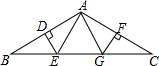 如图,在△ABC中,AB=AC,BC=12,∠BAC=120°,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点G,垂足分别为D,F.求∠EAG的度数和△AEG的周长.
如图,在△ABC中,AB=AC,BC=12,∠BAC=120°,AB的垂直平分线交BC边于点E,AC的垂直平分线交BC边于点G,垂足分别为D,F.求∠EAG的度数和△AEG的周长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
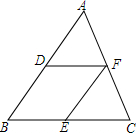 如图,DF、EF是△ABC的两条中位线.我们探究的问题是:这两条中位线和三角形的两条边所围成的四边形的形状与原三角形的边或角有什么关系.建议按下列步骤探索:
如图,DF、EF是△ABC的两条中位线.我们探究的问题是:这两条中位线和三角形的两条边所围成的四边形的形状与原三角形的边或角有什么关系.建议按下列步骤探索:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com