

���� ��1�������öԳƵ����ʼ��ɽ�����⣮����������������֮��С�ڵ������ɽ�����⣮
��2���ٵ�A����x��ĶԳƵ�A�䣨-2��-3�������ֱ��A��B���ɽ�����⣮�����ֱ��AB�Ľ���ʽ���ɽ�����⣮
��3��������$\sqrt{{a}^{2}+6a+13}+\sqrt{{b}^{2}+2b+10}$����Сֵ�����Կ�����x������һ��P��ʹ�õ�P����-3��4������-1��9���ľ���֮����С��
������$\sqrt{{b}^{2}+2b+10}-\sqrt{{a}^{2}+6a+13}$�����ֵ�����Կ�����x������һ��Q��ʹ��Q��A��-1��9����B��-3��4���ľ���֮�����
��� �⣺��1��������A����ֱ��m�ĶԳƵ�A�䣬����A��B��ֱ��l���ڵ�C����ʱAC+CB��С����C��ͼ��ʾ��
���ӳ�BA��ֱ��l��D����ʱDB-DA���D��ͼ��ʾ��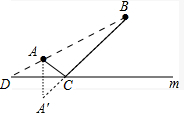
��2����A����x��ĶԳƵ�A�䣨-2��-3����
ֱ��A��B�Ľ���ʽΪy=$\frac{1}{3}$x-$\frac{1}{3}$��y=0ʱ��x=$\frac{4}{3}$��
���Ե�P���꣨$\frac{4}{3}$��0����PA+PB����Сֵ��$\sqrt{��5+3��^{2}+��4+2��^{2}}$=10��
ֱ��AB����ʽΪy=$\frac{1}{3}$x+$\frac{11}{3}$����y��Ľ���Ϊ��0��-11����
���Ե�P���꣨-11��0����PB-PA�����ֵΪ$\sqrt{��-2+11��^{2}+{3}^{2}}$=3$\sqrt{10}$��
��3���١�$\sqrt{{a}^{2}+6a+13}+\sqrt{{b}^{2}+2b+10}$=$\sqrt{��a+3��^{2}+4}$+$\sqrt{��b+1��^{2}+9}$��
����$\sqrt{{a}^{2}+6a+13}+\sqrt{{b}^{2}+2b+10}$����Сֵ��
���Կ�����x������һ��P��ʹ�õ�P����-3��4������-1��9���ľ���֮����С��
�ɣ�1����2����֪��Сֵ=$\sqrt{��9+4��^{2}+��-1+3��^{2}}$=$\sqrt{173}$��
�ڡ�$\sqrt{{b}^{2}+2b+10}-\sqrt{{a}^{2}+6a+13}$=$\sqrt{��b+1��^{2}+9}$-$\sqrt{��a+3��^{2}+4}$��
����$\sqrt{{b}^{2}+2b+10}-\sqrt{{a}^{2}+6a+13}$�����ֵ��
���Կ�����x������һ��Q��ʹ��Q��A��-1��9����B��-3��4���ľ���֮�����
��ֱ��AB����ʽΪy=$\frac{5}{2}$x+$\frac{23}{2}$����x�ύ�ڵ�Q��-$\frac{23}{5}$��0����
���ɣ�1����2����֪��ʱ���ֵ=$\frac{2\sqrt{41}}{5}$��
�ʴ�Ϊ��10��3$\sqrt{10}$��
���� ���⿼����Գơ�������ͼ�ε����ʵ�֪ʶ������Ĺؼ���ѧ�����öԳ�ȷ����ֵ���⣬ѧ��ת����˼��˼�����⣬�����п��������ͣ�


 ��������ϵ�д�
��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
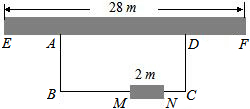 ��ͼ������һ��ǽ��ǽEF�������28�ף���Χ��һ�����λ�ABCD����ǽƽ�е�һ��BC��ҪԤ��2������ڣ���ͼ��MN��ʾ��������ǽ��������60�׳���ǽ�IJ��ϣ�
��ͼ������һ��ǽ��ǽEF�������28�ף���Χ��һ�����λ�ABCD����ǽƽ�е�һ��BC��ҪԤ��2������ڣ���ͼ��MN��ʾ��������ǽ��������60�׳���ǽ�IJ��ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AB��DE�ǡ�O��ֱ������C�ǡ�O�ϵ�һ�㣬��$\widehat{AD}$=$\widehat{CE}$����֤��BE=CE��
��ͼ��AB��DE�ǡ�O��ֱ������C�ǡ�O�ϵ�һ�㣬��$\widehat{AD}$=$\widehat{CE}$����֤��BE=CE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У���ABC�����������ֱ�ΪA��3��4����B��1��2����C��5��1����
��ͼ����ƽ��ֱ������ϵ�У���ABC�����������ֱ�ΪA��3��4����B��1��2����C��5��1�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com