
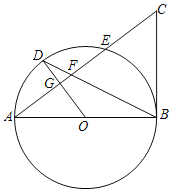
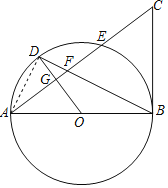
【题目】如图所示,AB是⊙O的直径,G为弦AE的中点,OG的延长线交⊙O于点D,连接BD交AE于点F,延长AE至点C,使得FC=BC,连接BC.
(1)求证:BC是⊙O的切线;
(2)⊙O的半径为10,tanA=![]() ,求BF的长.
,求BF的长.
【答案】(1)详见解析;(2)6![]() .
.
【解析】
(1)根据等腰三角形的性质得到∠ODB=∠OBD,∠CFB=∠CBF,由垂径定理得到OD⊥AE,推出CB⊥OB,于是得到BC是⊙O的切线;
(2)连接AD,根据圆周角定理得到∠ADB=90°,根据三角函数的定义得到OG=6,AG=8,由勾股定理得到![]() ,通过证明△AGD∽△DGF得到GF=2,
,通过证明△AGD∽△DGF得到GF=2,![]() ,于是得到结论.
,于是得到结论.
解:(1)∵OD=OB,FC=BC,
∴∠ODB=∠OBD,∠CFB=∠CBF,
∵G为弦AE的中点,且OD为半径,
∴OD⊥AE,
∴∠ODB+∠DFG=∠ODB+∠CFB=90°,
∴∠OBD+∠CBF=90°,即CB⊥OB,
∴BC是⊙O的切线;
(2)连接AD,
∵AB是⊙O的直径,
∴∠ADB=90°,
由![]() 可设OG=3x,AG=4x,
可设OG=3x,AG=4x,
在Rt△AOG中,
(3x)2+(4x)2=100,
∴x=2,
∴OG=6,AG=8,
∴![]() ,
,
∴![]() .
.
∵∠DAG+∠DFG=90°,∠GDF+∠DFG=90°,
∴∠DAG=∠GDF,
又∵∠DGF=∠AGD=90°,
∴△AGD∽△DGF,
∴![]() ,
,
∴GF=2,![]() ,
,
∴BF=BD﹣DF=6![]() .
.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:
【题目】为实施“农村留守儿童关爱计划”,某校结全校各班留守儿童的人数情况进行了统计,发现各班留守儿童人数只有1名、2名、3名、4名、5名、6名共六种情况,并制成如下两幅不完整的统计图:
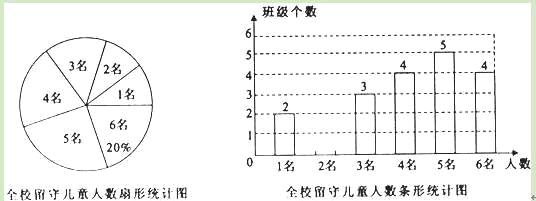
(1)求该校平均每班有多少名留守儿童?并将该条形统计图补充完整;
(2)某爱心人士决定从只有2名留守儿童的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名留守儿童来自同一个班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果公司以22元/千克的成本价购进1000kg苹果,公司想知道苹果的损坏率,随机抽取若干进行统计,部分结果如下表:
草果总质量n(kg) | 100 | 200 | 300 | 400 | 500 | 1000 |
损坏苹果质量m(kg) | 10.60 | 19.42 | 30.63 | 39.24 | 49.54 | 101.10 |
苹果损坏的频率 (结果保留小数点后三位) | 0.106 | 0.097 | 0.102 | 0.098 | 0.099 | 0.101 |
根据此表估计这批苹果损坏的概率(精确到0.1),从而计算该公司希望这批苹果能获得利润23000元,则销售时(去掉损坏的苹果)售价应至少定为_____元/千克.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,以AB为直径的⊙O交AC于点D,过点D作DE⊥BC于点E,且∠BDE=∠A.
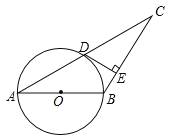
(1)判断DE与⊙O的位置关系,并说明理由;
(2)若AC=16,tanA=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
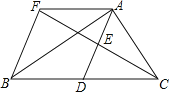
【题目】如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)求证:D是BC的中点;
(2)若BA⊥AC,试判断四边形AFBD的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
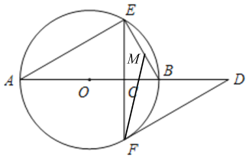
【题目】如图,AB是⊙O的直径,弦EF⊥AB,垂足为C,∠A=30°,连结BE,M为BE的中点,连结MF,过点F作直线FD∥AE,交AB的延长线于点D.
(1)求证:FD是⊙O的切线;
(2)若MF=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
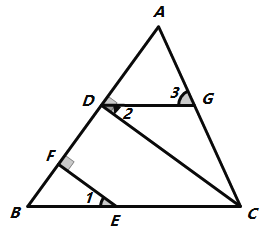
【题目】如图,在△ABC中,CD⊥AB,垂足为D. 点E在BC上,EF⊥AB,垂足为F,∠1=∠2.
(1)试说明DG∥BC的理由;
(2)如果∠B=54°,且∠ACD=35°,求的∠3度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b的图象与反比例函数y2=![]() 的图象交于A(2,3),B(6,n)两点.
的图象交于A(2,3),B(6,n)两点.
(1)分别求出一次函数与反比例函数的解析式;
(2)求△OAB的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com