


 x.
x.
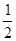 t,BN=
t,BN=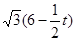 .
.
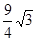
 x,那么PC=6-x.可表示出S△PCQ;
x,那么PC=6-x.可表示出S△PCQ;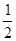 t,AB=12,那么BE=12-AD-DE=6-
t,AB=12,那么BE=12-AD-DE=6-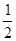 t.过E作EG⊥BN于点G.利用30°的三角函数可求得BG,进而求得BN,然后利用t表示出MC、CN,即可表示出所求面积,再求出S△MCN 的最大值。
t.过E作EG⊥BN于点G.利用30°的三角函数可求得BG,进而求得BN,然后利用t表示出MC、CN,即可表示出所求面积,再求出S△MCN 的最大值。

科目:初中数学 来源:不详 题型:解答题
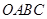 是一张放在平面直角坐标系中的矩形纸片,点
是一张放在平面直角坐标系中的矩形纸片,点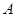 在
在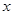 轴上,点
轴上,点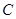 在
在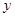 轴上,将边
轴上,将边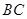 折叠,使点
折叠,使点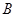 落在边
落在边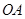 的点
的点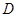 处.已知折叠
处.已知折叠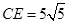 ,且
,且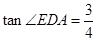 .
.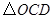 与
与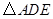 是否相似?请说明理由;
是否相似?请说明理由; 与
与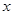 轴交点
轴交点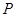 的坐标;
的坐标;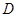 的直线
的直线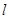 ,使直线
,使直线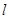 、直线
、直线 与
与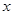 轴所围成的三角形和直线
轴所围成的三角形和直线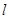 、直线
、直线 与
与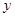 轴所围成的三角形相似?如果存在,请直接写出其解析式并画出相应的直线;如果不存在,请说明理由.
轴所围成的三角形相似?如果存在,请直接写出其解析式并画出相应的直线;如果不存在,请说明理由.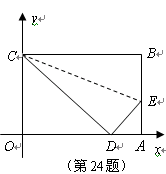
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 =90
=90 的垂直平分线EF交BC于点D,交AB于点E,且CF=AE
的垂直平分线EF交BC于点D,交AB于点E,且CF=AE
 的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.30 | B.32 | C.34 | D.16 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
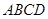 ,有以下四个条件:①
,有以下四个条件:①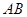 ∥
∥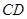 ;②
;②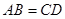 ;③
;③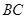 ∥
∥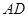 ;④
;④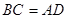 .从这四个条件中任选两个,能使四边形
.从这四个条件中任选两个,能使四边形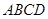 成为平行四边形的选法共有( )
成为平行四边形的选法共有( )| A.6种 | B.5种 | C.4种 | D.3种 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com