
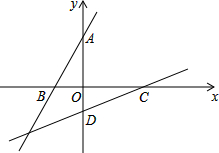
 已知A、B、C、D是平面坐标系中坐标轴上的点,且△AOB≌△COD.设直线AB的表达式为y1=k1x+b1,直线CD的表达式为y2=k2x+b2,则k1•k2=1.
已知A、B、C、D是平面坐标系中坐标轴上的点,且△AOB≌△COD.设直线AB的表达式为y1=k1x+b1,直线CD的表达式为y2=k2x+b2,则k1•k2=1. 分析 根据A(0,a)、B(b,0),得到OA=a,OB=-b,根据全等三角形的性质得到OC=a,OD=-b,得到C(a,0),D(0,b),求得k1=$\frac{a}{-b}$,k2=$\frac{-b}{a}$,即可得到结论.
解答 解:设点A(0,a)、B(b,0),
∴OA=a,OB=-b,
∵△AOB≌△COD,
∴OC=a,OD=-b,
∴C(a,0),D(0,b),
∴k1=$\frac{OA}{OB}$=$\frac{a}{-b}$,k2=$\frac{OD}{OC}$=$\frac{-b}{a}$,
∴k1•k2=1,
故答案为:1.
点评 本题考查了两直线相交与平行,全等三角形的性质,熟练掌握全等三角形的性质是解题的关键.


科目:初中数学 来源: 题型:解答题
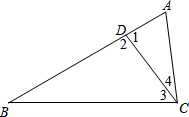 如图,△ABC中,D为AB上一点.已知△ADC与△DBC的面积比为1:3,且AD=3,AC=6,请求出BD的长度,并完整说明为何∠ACD=∠B的理由.
如图,△ABC中,D为AB上一点.已知△ADC与△DBC的面积比为1:3,且AD=3,AC=6,请求出BD的长度,并完整说明为何∠ACD=∠B的理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知双曲线y=$\frac{k}{x}$(k>0)经过Rt△OAB的直角边AB的中点C,与斜边OB相交于点D,若OD=1,则BD=$\sqrt{2}$-1.
如图,已知双曲线y=$\frac{k}{x}$(k>0)经过Rt△OAB的直角边AB的中点C,与斜边OB相交于点D,若OD=1,则BD=$\sqrt{2}$-1.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知点A是双曲线y=$\frac{5}{x}$在第三象限上的一动点,连接AO并延长交另一分支于点B,以AB为一边作等边三角形ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为y=-$\frac{15}{x}$.
已知点A是双曲线y=$\frac{5}{x}$在第三象限上的一动点,连接AO并延长交另一分支于点B,以AB为一边作等边三角形ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为y=-$\frac{15}{x}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
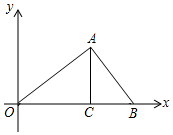 在如图所示的直角坐标系xOy中,AC⊥OB,OA⊥AB,OB=3,点C是OB上靠近O点的三等分点,若反比例函数y=$\frac{k}{x}$(x>0)的图象(图中未画出)与△OAB有两个交点,则k的取值范围是0<k<$\frac{9}{8}\sqrt{2}$.
在如图所示的直角坐标系xOy中,AC⊥OB,OA⊥AB,OB=3,点C是OB上靠近O点的三等分点,若反比例函数y=$\frac{k}{x}$(x>0)的图象(图中未画出)与△OAB有两个交点,则k的取值范围是0<k<$\frac{9}{8}\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com