
【题目】已知抛物线![]() 的顶点为点
的顶点为点![]() .
.
(1)求证:不论![]() 为何实数,该抛物线与
为何实数,该抛物线与![]() 轴总有两个不同的交点;
轴总有两个不同的交点;
(2)若抛物线的对称轴为直线![]() ,求
,求![]() 的值和
的值和![]() 点坐标;
点坐标;
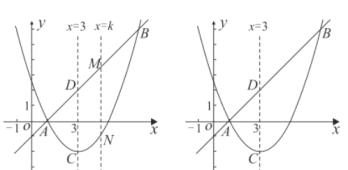
(3)如图,直线![]() 与(2)中的抛物线并于
与(2)中的抛物线并于![]() 两点,并与它的对称轴交于点
两点,并与它的对称轴交于点![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() ,交抛物线于点
,交抛物线于点![]() .求当
.求当![]() 为何值时,以
为何值时,以![]() 为顶点的四边形为平行四边形.
为顶点的四边形为平行四边形.
【答案】(1)详见解析;(2)![]() ,点
,点![]() 坐标为
坐标为![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() 时,可使得
时,可使得![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.
【解析】
(1)从![]() 的判别式出发,判别式总大于等于3,而证得;
的判别式出发,判别式总大于等于3,而证得;
(2)根据抛物线的对称轴![]() 来求
来求![]() 的值;然后利用配方法把抛物线解析式转化为顶点式,由此可以写出点
的值;然后利用配方法把抛物线解析式转化为顶点式,由此可以写出点![]() 的坐标;
的坐标;
(3)根据平行四边形的性质得到:![]() .
.
需要分类讨论:①当四边形![]() 是平行四边形,
是平行四边形,![]() ,通过解该方程可以求得
,通过解该方程可以求得![]() 的值;
的值;
②当四边形![]() 是平行四边形,
是平行四边形,![]() ,通过解该方程可以求得
,通过解该方程可以求得![]() 的值.
的值.
解:(1)![]() ,
,
∵不论![]() 为何实数,总有
为何实数,总有![]() ,
,
![]() ,
,
∴无论![]() 为何实数,关于
为何实数,关于![]() 的一元二次方程
的一元二次方程![]() 总有两个不相等的实数根,
总有两个不相等的实数根,
∴无论![]() 为何实数,抛物线
为何实数,抛物线![]() 与
与![]() 轴总有两个不同的交点.
轴总有两个不同的交点.
(2)![]() 抛物线的对称轴为直线
抛物线的对称轴为直线![]() ,
,
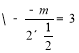 ,即
,即![]() ,
,
此时,抛物线的解析式为![]() ,
,
∴顶点![]() 坐标为
坐标为![]() ;
;
(3)![]() 为顶点的四边形是平行四边形,
为顶点的四边形是平行四边形,
![]() 四边形
四边形![]() 是平行四边形(直线在抛物线的上方)或四边形
是平行四边形(直线在抛物线的上方)或四边形![]() (直线在抛物线的下方),如图所示,
(直线在抛物线的下方),如图所示,
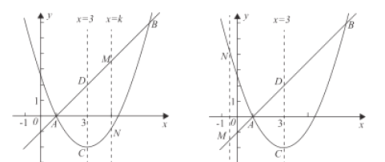
由已知![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
①当四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,
整理得,![]() ,
,
解得![]() (不合题意,舍去),
(不合题意,舍去),![]() ;
;
②当四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,
整理得![]() ,
,
解得,![]() ,
,
综上,![]() 或
或![]() 或
或![]() 时,可使得
时,可使得![]() 为顶点的四边形是平行四边形.
为顶点的四边形是平行四边形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
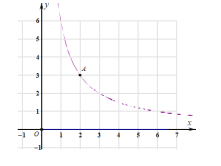
【题目】如图,在平面直角坐标系 xOy中,反比例函数 y ![]() x 0 的图象经过点 A2,3 ,直线y ax , y
x 0 的图象经过点 A2,3 ,直线y ax , y ![]() 与反比例函数 y
与反比例函数 y ![]() x 0 分别交于点 B,C两点.
x 0 分别交于点 B,C两点.
(1)直接写出 k 的值 ;
(2)由线段 OB,OC和函数 y ![]() x 0 在 B,C 之间的部分围成的区域(不含边界)为 W.
x 0 在 B,C 之间的部分围成的区域(不含边界)为 W.
① 当 A点与 B点重合时,直接写出区域 W 内的整点个数 ;
② 若区域 W内恰有 8个整点,结合函数图象,直接写出 a的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线交x轴于A,B两点(A在B右边),A(3,0),B(1,0)交y轴于C点,C(0,3),连接AC;
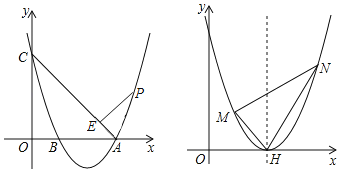
(1)求抛物线的解析式;
(2)P为抛物线上的一点,作PE⊥CA于E点,且CE=3PE,求P点坐标;
(3)将原抛物线向上平移1个单位抛物线的对称轴交x轴于H点,过H作直线MH,NH,当MH⊥NH时,求MN恒过的定点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】身高1.65米的兵兵在建筑物前放风筝,风筝不小心挂在了树上.在如图所示的平面图形中,矩形CDEF代表建筑物,兵兵位于建筑物前点B处,风筝挂在建筑物上方的树枝点G处(点G在FE的延长线上).经测量,兵兵与建筑物的距离BC=5米,建筑物底部宽FC=7米,风筝所在点G与建筑物顶点D及风筝线在手中的点A在同一条直线上,点A距地面的高度AB=1.4米,风筝线与水平线夹角为37°.
(1)求风筝距地面的高度GF;
(2)在建筑物后面有长5米的梯子MN,梯脚M在距墙3米处固定摆放,通过计算说明:若兵兵充分利用梯子和一根米长的竹竿能否触到挂在树上的风筝?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
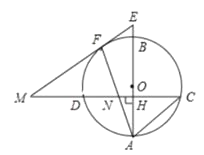
【题目】如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,在CD上有点N满足CN=CA,AN交圆O于点F,过点F的AC的平行线交CD的延长线于点M,交AB的延长线于点E.
(1)求证:EM是圆O的切线;
(2)若AC:CD=5:8,AN=3![]() ,求圆O的直径长度.
,求圆O的直径长度.
(3)在(2)的条件下,直接写出FN的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尼泊尔发生了里氏8.1级地震,某中学组织了献爱心捐款活动,该校教学兴趣小组对本校学生献爱心捐款额做了一次随机抽样调查,并绘制了不完整的频数分布表和频数分布直方图.如图所示:

(1)a等于多少?b等于多少?
(2)补全频数分布直方图;若制成扇形统计图,求捐款额在![]() 之间的扇形圆心角的度数;
之间的扇形圆心角的度数;
(3)该校共有1600名学生,估计这次活动中爱心捐款额不低于20元的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=![]() (x>0)的图象经过点C,交AB于点D.已知AB=4,BC=
(x>0)的图象经过点C,交AB于点D.已知AB=4,BC=![]() .
.
(1)若OA=4,求k的值;
(2)连接OC,若BD=BC,求OC的长.
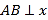
查看答案和解析>>
科目:初中数学 来源: 题型:
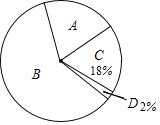
【题目】某中学的一个数学兴趣小组在本校学生中开展了主题为“雾霾知多少”的专题调查括动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“A.非常了解”、“B.比较了解”、“C.基本了解”、“D.不太了解”四个等级,将所得数据进行整理后,绘制成如下两幅不完整的统计图表,请你结合图表中的信息解答下列问题
等级 | A | B | C | D |
频数 | 40 | 120 | 36 | n |
频率 | 0.2 | m | 0.18 | 0.02 |
(1)表中m= ,n= ;
(2)扇形统计图中,A部分所对应的扇形的圆心角是 °,所抽取学生对丁雾霾了解程度的众数是 ;
(3)若该校共有学生1500人,请根据调查结果估计这些学生中“比较了解”人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某中学学生课余生活情况,对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计,现从该校随机抽取n名学生作为样本,采用问卷调查的方式收集数据![]() 参与问卷调查的每名学生只能选择其中一项
参与问卷调查的每名学生只能选择其中一项![]() ,并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图,由图中提供的信息,解答下列问题:
,并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图,由图中提供的信息,解答下列问题:
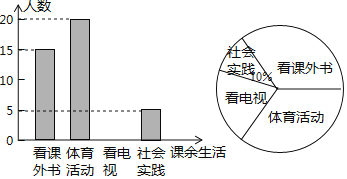
![]() 补全条形统计图;
补全条形统计图;
![]() 若该校共有学生2400名,试估计该校喜爱看电视的学生人数.
若该校共有学生2400名,试估计该校喜爱看电视的学生人数.
![]() 若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名,求恰好抽到2名男生的概率.
若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名,求恰好抽到2名男生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com