
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��ı���OABC�Ķ���O������ԭ�㣬��A�ڵ�һ���ޣ���C�ڵ������ޣ���B��x����������ϣ���OAB=90����OA=AB��OB��OC�ij��ֱ���һԪ���η���x2��11x+30=0����������OB��OC����
��1�����A�͵�B�����꣮
��2����P���߶�OB�ϵ�һ�����㣨��P�����O��B�غϣ�������P��ֱ��l��y��ƽ�У�ֱ��l����OA���AB�ڵ�Q������OC���BC�ڵ�R�����P�ĺ�����Ϊt���߶�QR�ij���Ϊm����֪t=4ʱ��ֱ��lǡ�ù���C����0��t��3ʱ����m����t�ĺ�����ϵʽ��
��3����m=3.5ʱ����ֱ��д����P�����꣮
���𰸡�
��1��
�⣺�߷���x2��11x+30=0�Ľ�Ϊx1=5��x2=6��
��OB=6��OC=5��
��B��������6��0����
��AM��x����M����ͼ��
�ߡ�OAB=90����OA=AB��
���AOBΪ����ֱ�������Σ�
��OM=BM=AM= ![]() OB=3��
OB=3��
��B��������3��3����
��2��
�⣺��CN��x����N����ͼ��
��t=4ʱ��ֱ��lǡ�ù���C��
��ON=4��
��Rt��OCN��CN= ![]() =
= ![]() =3��
=3��
��C��������4����3����
��ֱ��OC�Ľ���ʽΪy=kx��
��C��4����3�������4k=��3�����k=�� ![]() ��
��
��ֱ��OC�Ľ���ʽΪy=�� ![]() x��
x��
��ֱ��OA�Ľ���ʽΪy=ax��
��A��3��3�������3a=3�����a=1��
��ֱ��OA�Ľ���ʽΪy=x��
��P��t��0����0��t��3����
��Q��t��t����R��t���� ![]() t����
t����
��QR=t������ ![]() t��=
t��= ![]() t��
t��
��m= ![]() t��0��t��3����
t��0��t��3����
��3��
�⣺��ֱ��AB�Ľ���ʽΪy=px+q��
��A��3��3����B��6��0������� ![]() �����
����� ![]() ��
��
��ֱ��AB�Ľ���ʽΪy=��x+6��
ͬ���ɵ�ֱ��BC�Ľ���ʽΪy= ![]() x��9��
x��9��
��0��t��3ʱ��m= ![]() t����m=3.5����
t����m=3.5���� ![]() t=3.5�����t=2����ʱP������Ϊ��2��0����
t=3.5�����t=2����ʱP������Ϊ��2��0����
��3��t��4ʱ��Q��t����t+6����R��t���� ![]() t����
t����
��m=��t+6������ ![]() t��=��
t��=�� ![]() t+6����m=3.5����
t+6����m=3.5���� ![]() t+6=3.5�����t=10������������ȥ����
t+6=3.5�����t=10������������ȥ����
��4��t��6ʱ��Q��t����t+6����R��t�� ![]() t��9����
t��9����
��m=��t+6���� ![]() t��9��=��
t��9��=�� ![]() t+15����m=3.5����
t+15����m=3.5���� ![]() t+15=3.5�����t=
t+15=3.5�����t= ![]() ����ʱP������Ϊ��
����ʱP������Ϊ�� ![]() ��0����
��0����
��������������������P��������2��0���� ![]() ��0����
��0����

�����������⿼�����ı��ε��ۺ��⣺�������յ���ֱ�������ε����ʺ�һ�κ���ͼ���ϵ�����������������ô���ϵ������һ�κ�������ʽ������������ͼ�����ʣ������õ�������ʾ�߶εij���ѧ�����÷������۵�˼������ѧ���⣮��1����������ʽ�ֽⷨ�ⷽ��x2��11x+30=0�ɵõ�OB=6��OC=5����B������Ϊ��6��0������AM��x����M����ͼ�����õ���ֱ�������ε����ʵ�OM=BM=AM= ![]() OB=3�����ǿ�д��B�����ꣻ��2����CN��x����N����ͼ�������ù��ɶ��������CN�õ�C������Ϊ��4����3���������ô���ϵ�����ֱ����ֱ��OC�Ľ���ʽΪy=��
OB=3�����ǿ�д��B�����ꣻ��2����CN��x����N����ͼ�������ù��ɶ��������CN�õ�C������Ϊ��4����3���������ô���ϵ�����ֱ����ֱ��OC�Ľ���ʽΪy=�� ![]() x��ֱ��OA�Ľ���ʽΪy=x�������һ�κ���ͼ���ϵ�����������õ�Q��t��t����R��t����
x��ֱ��OA�Ľ���ʽΪy=x�������һ�κ���ͼ���ϵ�����������õ�Q��t��t����R��t���� ![]() t��������QR=t������
t��������QR=t������ ![]() t�����Ӷ��õ�m����t�ĺ�����ϵʽ����3�����ô���ϵ�������ֱ��AB�Ľ���ʽΪy=��x+6��ֱ��BC�Ľ���ʽΪy=
t�����Ӷ��õ�m����t�ĺ�����ϵʽ����3�����ô���ϵ�������ֱ��AB�Ľ���ʽΪy=��x+6��ֱ��BC�Ľ���ʽΪy= ![]() x��9��Ȼ��������ۣ���0��t��3ʱ������
x��9��Ȼ��������ۣ���0��t��3ʱ������ ![]() t=3.5�����t�õ�P�����ꣻ
t=3.5�����t�õ�P�����ꣻ
��3��t��4ʱ����Q��t����t+6����R��t���� ![]() t�������ǵõ���t+6������
t�������ǵõ���t+6������ ![]() t��=3.5�����t=10��������t�ķ�Χ��ȥ����4��t��6ʱ����Q��t����t+6����R��t��
t��=3.5�����t=10��������t�ķ�Χ��ȥ����4��t��6ʱ����Q��t����t+6����R��t�� ![]() t��9�������ԩ�t+6����
t��9�������ԩ�t+6���� ![]() t��9��=3.5��Ȼ��ⷽ�����t�õ�P�����꣮
t��9��=3.5��Ȼ��ⷽ�����t�õ�P�����꣮
�����㾫����ͨ��������õ���ֱ�������κ�ȷ��һ�κ����ı���ʽ�����յ���ֱ��������������ֱ�DZ���ȵ�ֱ�������Σ�����ֱ�������ε�����������ҵ���45�㣻ȷ��һ��һ�κ�������Ҫȷ��һ�κ�������ʽy=kx+b��k������0���еij���k��b�������������һ�㷽���Ǵ���ϵ���������Խ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)��֪a��b����![]() �������x�ķ���(a��2)x��b2��a��1��
�������x�ķ���(a��2)x��b2��a��1��
(2)ʵ��a��b��Ϊ�෴����c��d��Ϊ������x�ľ���ֵΪ![]() �������ʽx2��(a��b)cdx��
�������ʽx2��(a��b)cdx��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڲ���ʽ��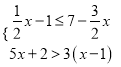 ����˵����ȷ���ǣ�������
����˵����ȷ���ǣ�������
A. �˲���ʽ���� B. �˲���ʽ����7��������
C. �˲���ʽ��ĸ��������ǩ�3����2����1 D. �˲���ʽ��Ľ⼯��![]() ��x��2
��x��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����P��ƽ���ı���ABCD�Խ���AC����ֱ���ϵ�һ�����㣨��P�����A��C�غϣ����ֱ����A��C��ֱ��BP�����ߣ�����ֱ�Ϊ��E��F����OΪAC���е㣮
��1������P���O�غ�ʱ��ͼ1����֤OE=OF������֤����
��2��ֱ��BP�Ƶ�B��ʱ�뷽����ת������OFE=30��ʱ����ͼ2��ͼ3��λ�ã������߶�CF��AE��OE֮����������������ϵ����д�����ͼ2��ͼ3�IJ��룬��ѡ��һ���������֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ѧ��55�ˣ�����������Ů��������֮��Ϊ6��5��
��1������ð�������Ů����������
��2��ѧУҪ�Ӹð�ѡ��20�˲μ�ѧУ�ĺϳ��ţ�Ҫ������������������7�ˣ���Ů����������������
��2�����ϡ������С�Ů�������м���ѡ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���BAD=120�㣬��E��F�ֱ��ڱ�AB��BC�ϣ���BEF���GEF����ֱ��EF�Գƣ���B�ĶԳƵ��ǵ�G���ҵ�G�ڱ�AD�ϣ���EG��AC��AB=6 ![]() ����FG�ij�Ϊ ��
����FG�ij�Ϊ �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�ٰ���һ�γ���֪ʶ����������10�֣�ѧ���÷־�Ϊ�������ɼ��ﵽ6�ּ�6������Ϊ�ϸﵽ9�ֻ�10��Ϊ����.��ξ����мס�������ѧ���ɼ��ֲ�������ͳ��ͼ�ͳɼ�ͳ�Ʒ�������ͼ��ʾ.

��1��������гɼ�ͳ�Ʒ�������![]() ��ֵ��
��ֵ��
��2��СӢͬѧ˵������ξ����ҵ���7�֣�������С�����������������ϣ����۲���������жϣ�СӢ�Ǽס����ĸ����ѧ����
��3������ͬѧ˵������ĺϸ��ʡ������ʾ��������飬����������ijɼ��������飬������ͬѧ��ͬ�����ͬѧ��˵������Ϊ���ǵijɼ�Ҫ���ڼ���.�����������֧������ͬѧ�۵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��AOB�У���AOB=90�㣬OA=3��OB=2����Rt��AOB�Ƶ�O˳ʱ����ת90����Rt��FOE�����߶�EF�Ƶ�E��ʱ����ת90�����߶�ED���ֱ���O��EΪԲ�ģ�OA��ED��Ϊ�뾶����AF�ͻ�DF������AD����ͼ����Ӱ��������ǣ������� 
A.��
B.![]()
C.3+��
D.8����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com