
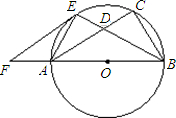
 如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交
如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠B的平分线BE交AC于D,交| AE |
| BE |
| AF |
| EF |
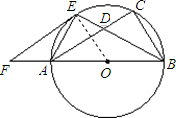 解:(1)直线EF与⊙O相切.
解:(1)直线EF与⊙O相切.| FE |
| FA |
| FB |
| FE |
| AE |
| BE |
| AF |
| EF |
| 5 |


 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案科目:初中数学 来源: 题型:
 23、如图,已知以Rt△ABC的直角边AB为直径作⊙O与斜边AC交于点D,E为BC边的中点,连接DE,
23、如图,已知以Rt△ABC的直角边AB为直径作⊙O与斜边AC交于点D,E为BC边的中点,连接DE,查看答案和解析>>
科目:初中数学 来源: 题型:
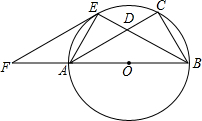 如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠ABC的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.
如图,已知以Rt△ABC的边AB为直径作△ABC的外接圆⊙O,∠ABC的平分线BE交AC于D,交⊙O于E,过E作EF∥AC交BA的延长线于F.查看答案和解析>>
科目:初中数学 来源: 题型:
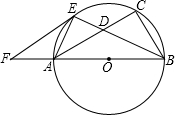 ∥AC交BA的延长线于F.
∥AC交BA的延长线于F.查看答案和解析>>
科目:初中数学 来源:2013届湖北省襄阳市襄城区中考适应性考试数学试卷(带解析) 题型:解答题
如图,已知以Rt△ABC的直角边AB为直径做圆O,与斜边AC交于点D,E为BC边的中点,连接DE.
(1)求证:DE是⊙O的切线;
(2)连接OE、AE,当∠CAB为何值时,四边形AODE是平行四边形,并说明理由;
(3)在(2)的条件下,求sin∠CAE的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com