
【题目】(1)问题发现:
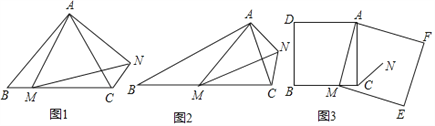
如图1,在等边三角形ABC中,点M为BC边上异于B、C的一点,以AM为边作等边三角形AMN,连接CN,NC与AB的位置关系为__________;
(2)深入探究:
如图2,在等腰三角形ABC中,BA=BC,点M为BC边上异于B、C的一点,以AM为边作等腰三角形AMN,使∠ABC=∠AMN,AM=MN,连接CN,试探究∠ABC与∠ACN的数量关系,并说明理由;
(3)拓展延伸:
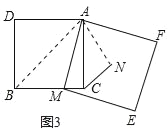
如图3,在正方形ADBC中,AD=AC,点M为BC边上异于B、C的一点,以AM为边作正方形AMEF,点N为正方形AMEF的中点,连接CN,若BC=10,CN=![]() ,试求EF的长.
,试求EF的长.
【答案】(1)NC∥AB(2)∠ABC=∠ACN,理由见解析;(3)EF= ![]() .
.
【解析】分析:(1)根据△ABC,△AMN为等边三角形,得到AB=AC,AM=AN且∠BAC=∠MAN=60°从而得到∠BAC-∠CAM=∠MAN-∠CAM,即∠BAM=∠CAN,证明△BAM≌△CAN,即可得到BM=CN.
(2)根据△ABC,△AMN为等腰三角形,得到AB:BC=1:1且∠ABC=∠AMN,根据相似三角形的性质得到![]() ,利用等腰三角形的性质得到∠BAC=∠MAN,根据相似三角形的性质即可得到结论;
,利用等腰三角形的性质得到∠BAC=∠MAN,根据相似三角形的性质即可得到结论;
(3)如图3,连接AB,AN,根据正方形的性质得到∠ABC=∠BAC=45°,∠MAN=45°,根据相似三角形的性质得出![]() ,得到BM=2,CM=8,再根据勾股定理即可得到答案.
,得到BM=2,CM=8,再根据勾股定理即可得到答案.
详解:(1)NC∥AB,理由如下:
∵△ABC与△MN是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAM=∠CAN,
在△ABM与△ACN中,
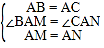 ,
,
∴△ABM≌△ACN(SAS),
∴∠B=∠ACN=60°,
∵∠ANC+∠ACN+∠CAN=∠ANC+60°+∠CAN=180°,
∴∠ANC+∠MAN+∠BAM=∠ANC+60°+∠CAN=∠BAN+∠ANC=180°,
∴CN∥AB;
(2)∠ABC=∠ACN,理由如下:
∵![]() =1且∠ABC=∠AMN,
=1且∠ABC=∠AMN,
∴△ABC~△AMN
∴![]() ,
,
∵AB=BC,
∴∠BAC=![]() (180°﹣∠ABC),
(180°﹣∠ABC),
∵AM=MN
∴∠MAN=![]() (180°﹣∠AMN),
(180°﹣∠AMN),
∵∠ABC=∠AMN,
∴∠BAC=∠MAN,
∴∠BAM=∠CAN,
∴△ABM~△ACN,
∴∠ABC=∠ACN;
(3)如图3,连接AB,AN,
∵四边形ADBC,AMEF为正方形,
∴∠ABC=∠BAC=45°,∠MAN=45°,
∴∠BAC﹣∠MAC=∠MAN﹣∠MAC
即∠BAM=∠CAN,
∵![]() ,
,
∴![]() ,
,
∴△ABM~△ACN
∴![]() ,
,
∴![]() =cos45°=
=cos45°=![]() ,
,
∴![]() ,
,
∴BM=2,
∴CM=BC﹣BM=8,
在Rt△AMC,
AM=![]() ,
,
∴EF=AM=2![]() .
.


 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:初中数学 来源: 题型:
【题目】(1)模型建立:
如图,等腰直角三角形![]() 中,
中,![]() ,
,![]() ,直线
,直线![]() 经过点
经过点![]() ,过
,过![]() 作
作![]() 于
于![]() ,过
,过![]() 作
作![]() 于
于![]() .求证:
.求证:![]() ;
;
(2)模型应用:
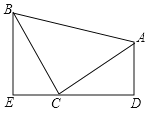
①如图,一次函数![]() 的图象分别与
的图象分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() 、
、![]() ,以线段
,以线段![]() 为腰在第一象限内作等腰直角三角形
为腰在第一象限内作等腰直角三角形![]() ,则
,则![]() 点的坐标为___________(直接写出结果)
点的坐标为___________(直接写出结果)
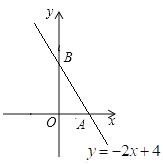
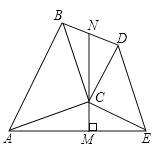
②如图,在![]() 和
和![]() 中,
中,![]() ,
,![]() ,
,![]() ,连接
,连接![]() 、
、![]() ,作
,作![]() 于
于![]() 点,延长
点,延长![]() 与
与![]() 交于点
交于点![]() ,求证:
,求证:![]() 是
是![]() 的中点.
的中点.
查看答案和解析>>
科目:初中数学 来源: 题型:
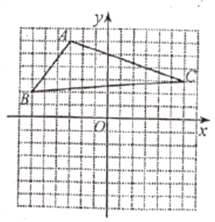
【题目】如图,![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() 、
、![]() 、
、![]() .
. ![]() 与
与![]() 关于
关于![]() 轴对称,
轴对称,![]() 与
与![]() 关于
关于![]() 轴对称,点
轴对称,点![]() 、
、![]() 、
、![]() 分别是点
分别是点![]() 、
、![]() 、
、![]() 的对应点,点
的对应点,点![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 的对应点.
的对应点.
(1)画出![]() 与
与![]() ,并写出点
,并写出点![]() 、
、![]() 、
、![]() 的坐标;
的坐标;
(2)连接![]() 、
、![]() ,求六边形
,求六边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,在边
,在边![]() 上顺次取点
上顺次取点![]() ,
,![]() ,
,![]() …,在边
…,在边![]() 上顺次取点
上顺次取点![]() ,
,![]() ,
,![]() …,使得
…,使得![]() …,得到等腰△
…,得到等腰△![]() ,△
,△![]() ,△
,△![]() ,△
,△![]() …
…

(1)若![]() =30°,可以得到的最后一个等腰三角形是_________;
=30°,可以得到的最后一个等腰三角形是_________;
(2)若按照上述方式操作,得到的最后一个等腰三角形是△![]() ,则
,则![]() 的度数
的度数![]() 的取值范围是________.
的取值范围是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
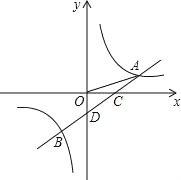
【题目】如图,一次函数y=ax+b的图象与反比例函数![]() 的图象交于A,B两点,与X轴交于点C,与Y轴交于点D,已知
的图象交于A,B两点,与X轴交于点C,与Y轴交于点D,已知![]() ,A(n,1),点B的坐标为(﹣2,m)
,A(n,1),点B的坐标为(﹣2,m)
(1)求反比例函数的解析式和一次函数的解析式;
(2)连结BO,求△AOB的面积;
(3)观察图象直接写出一次函数的值大于反比例函数的值时x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
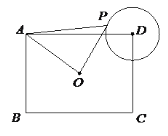
【题目】如图,在矩形ABCD中,AB=3,BC=4,O为矩形ABCD的中心,以D为圆心1为半径作⊙D,P为⊙D上的一个动点,连接AP、OP,则△AOP面积的最大值为( )
A. 4 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,点B,D在⊙O上,点E在⊙O外,∠EAB=∠D=30°.
(1)∠C的度数为 ;
(2)求证:AE是⊙O的切线;
(3)当AB=3时,求图中阴影部分的面积(结果保留根号和π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.

(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为________;
(2)小明先转动转盘一次,当转盘停止转动时,记录下指针所指扇形中的数字;接着再转动转盘一次,当转盘停止转动时,再次记录下指针所指扇形中的数字,求这两个数字之和是3的倍数的概率(用画树状图或列表等方法求解)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com