练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．解方程
    （1）x2+27=12x
    （2）3x2-2x-4=0．

    分析 （1）因式分解法求解可得；
    （2）公式法求解可得．

    解答 解：（1）x2-12x+27=0，
    ∴（x-3）（x-9）=0，
    ∴x-3=0或x-9=0，
    解得：x=3或x=9；

    （2）∵a=3，b=-2，c=-4，
    ∴△=4-4×3×（-4）=52＞0，
    ∴x=$\frac{2±2\sqrt{13}}{2×3}$=$\frac{1±\sqrt{13}}{3}$．

    点评 本题主要考查解一元二次方程的能力，熟练掌握解一元二次方程的几种常用方法：直接开平方法、因式分解法、公式法、配方法，结合方程的特点选择合适、简便的方法是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    1．计算：$\frac{2a}{5{a}^{2}b}$+$\frac{3b}{10ab}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    2．下列计算，正确的是（　　）
    A．$\sqrt{{{（-2）}^2}}=-2$B．$\sqrt{（-2）×（-2）}=2$C．$3\sqrt{2}-\sqrt{2}=3$D．$\sqrt{8}+\sqrt{2}=\sqrt{10}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

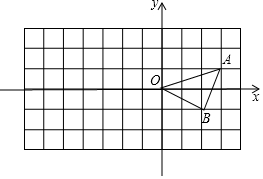    19．方格纸中每个小正方形的边长都是单位1，△OAB在平面直角坐标系中的位置如图所示．解答问题：
    （1）请按要求对△ABO作如下变换：
    ①将△OAB向下平移2个单位，再向左平移3个单位得到△O1A1B1；
    ②以点O为位似中心，位似比为2：1，将△ABC在位似中心的异侧进行放大得到△OA2B2．
    （2）写出点A1，A2的坐标：（0，-1），（-6，-2）；
    （3）△OA2B2的面积为10．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．在平面直角坐标系xOy中，抛物线y=-2x2+bx+c经过点A（0，2），B（3，-4）．
    （1）求抛物线的表达式及对称轴；
    （2）设点B关于原点的对称点为C，点D是抛物线对称轴上一动点，记抛物线在A，B之间的部分为图象G（包含A，B两点）．若直线CD与图象G有公共点，结合函数图象，求点D纵坐标t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．将下列平面图形绕轴旋转一周，可得到图中所示的立体图形的是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．如果一些体积为1cm3的小立方体恰好可以组成体积为1m3的大立方体，把所有这些小立方体一个接一个向上摞起来，大概有多高呢？以下选项中最接近这一高度的是（　　）
    A．天安门城楼高度B．未来北京最高建筑“中国尊”高度
    C．五岳之首泰山高度D．国际航班飞行高度

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．先化简，再求值：$\frac{{a}^{2}-1}{{a}^{2}+2a+1}$÷$\frac{{a}^{2}-a}{a+1}$，其中a=$\sqrt{27}$-$\sqrt{12}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．（1）-0.2的相反数为0.2，倒数是-5．
    （2）若一个数的倒数为-$\frac{3}{2}$，则这个数的相反数为$\frac{2}{3}$．
    （3）一个数与它的倒数相等，那么这个数是±1．
    （4）若一个数的绝对值为4$\frac{1}{3}$，则这个数的倒数为±$\frac{3}{13}$．

    查看答案和解析>>

    同步练习册答案