
分析 (1)直接利用二次根式的性质化简求出即可;
(2)直接利用二次根式的性质化简求出即可.
解答 解:(1)b$\sqrt{\frac{3b}{a}}•\sqrt{\frac{3{a}^{2}}{b}}$=b$\sqrt{\frac{3b}{a}×\frac{3{a}^{2}}{b}}$=3b$\sqrt{a}$(a>0,b>0);
故答案为:3b$\sqrt{a}$;
(2)$\frac{2\sqrt{{m}^{2}n}}{3\sqrt{mn}}$=$\frac{2\sqrt{mn}×\sqrt{m}}{3\sqrt{mn}}$=$\frac{2\sqrt{m}}{3}$(m>0,n>0).
故答案为:$\frac{2\sqrt{m}}{3}$.
点评 此题主要考查了二次根式的乘除法运算,正确化简二次根式是解题关键.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
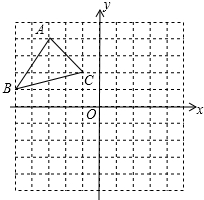 如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
如图,方格纸中每个小正方形的边长都是单位1,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连接AD1、BC1.若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分面积为S,则下列结论:
如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连接AD1、BC1.若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分面积为S,则下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
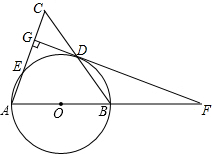 如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,DG⊥AC于点G,交AB的延长线于点F.
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,DG⊥AC于点G,交AB的延长线于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com